交叉の実装例

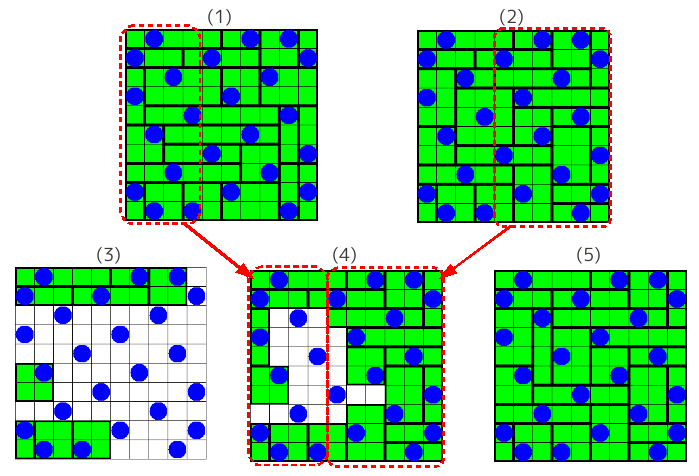
（１）、（２）が、親となる２つの染色体である。
（３）が、（１）、（２）の完全一致部分だけをコピーしたものである。

ここまでを前回示した。

ここでは、交叉を次のように考えた。
2つの親(1)(2)を重ねて、同じ箇所で切断し、できた断片を、異なる親通しを結合してみた。
切断方向、切断位置は、乱数で適当に決めている。

例では、(1)の左側と、(2)の右側が子染色体にそのまま引き継がれるとした。
切断線で切られる長方形は無視し、(1)の左側に完全に含まれている全長方形と、(2)の右側に完全に含まれている長方形を、子にコピーすることで、(3）から(4)が得られた。

未決定部分は、空白のままになっている。空白部分は、切断線付近にだけできるはずである。

さて、この空白部分を適当に切り分け直して、盤面全体が長方形で分割されるようにすると、新たな長方形分割が完成する。これに関しては、核を含む長方形を適当に上下左右に拡大していくとことで、盤面全体を覆い尽くすことができる。
もしうまくいかなければ、(4)から再度繰り返すことで、たぶんそのうちできるようであった。

これが、長方形分割に対する、遺伝的アルゴリズムの交叉処理の１つの実装である。

遺伝的アルゴリズムを用いる場合、問題を解決するためのアルゴリズム自体を考える必要はほとんどなくなる。しかし、交叉や突然変異をどう実装するかという新たな問題が発生し、この実装方法次第で、速度、品質などに大差ができてしまう。

遺伝的アルゴリズムは、通常の方法では手に負えないような、非数値的な問題にこそ真価を発揮する。しかし、このあたりが書籍等にはほとんど書かれていないのが残念である。