前回、ひとり遊び「計算」のルールを説明したが、実際にプレイしたであろうか。
次図に、実際のプレイの終盤の状態を示す。
手札はT(10)が見えていて、まだ表になっていな手札が1枚だけ残って、それが4である。
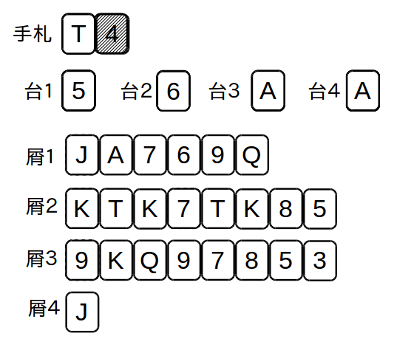
この状態から、手札、屑札の全てのカードを、台札の上に全て重ねることができ、成功するのであるが、その順番は分かるであろうか
実際には、成功可能な状態になっているのに、失敗してしまうことが多いであろう。
失敗しないためには、どういう戦略を立てれば良いだろうか。
台札の上に重ねるにに、A−2−3−、2−4−6−、3−6−9−、4−8−Q−の順(正順)に考えるのではなく、次図のように、各台札について逆順列を用意し、屑札の上のカードが、この順序に並ぶようにすると良い。

屑札の上に重なったカードは、この逆順にうまくつながっていれば、いくら重なっていても気にする必要はなく、最後はするすると全部取り出せて台札の上に重ねられ成功となる。
次図に、それぞれのカードをどの台札の上に載せることになるのか丸付き数字で示した。丸の中の1〜4は、載せる台札の山の番号を示す。
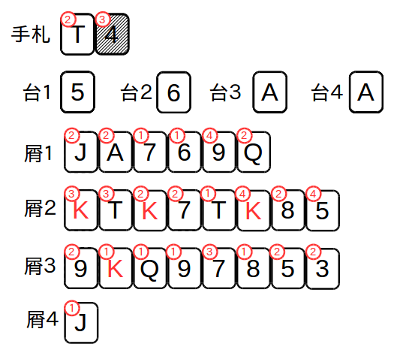
でも、これでは分かりにくいだろうから、この順番に糸が絡むことなく取り出せることを下図に示す。
屑札は、適当に間を開け配置したので、右端から順に取り出し、台札に載せられることが分かりやすくなっただろうか。
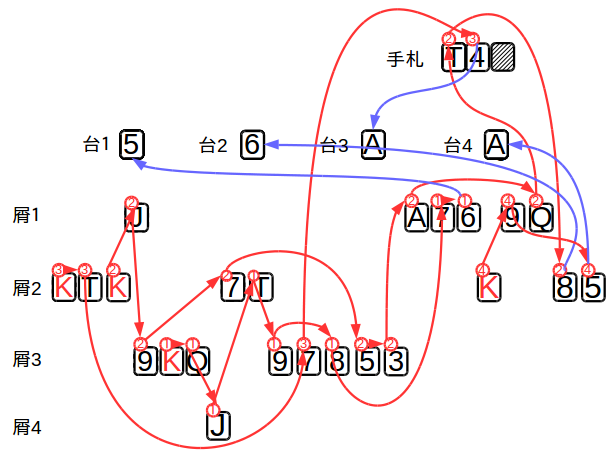
このように綺麗に最後が片付くためには、そうなるように屑札の上にカードを重ねないといけない。
ここで、最後に一気に取り出せたカードは、どのようにして上手く重なっていたのか、最初の方を見てみよう。
次図が最初の20手までのカードの動きである。丸数字は、手番号を示す。
4手目でQを屑4に出しているが、17手目で台4に重ねることで、屑4にカードが一旦無くなったことを示す。
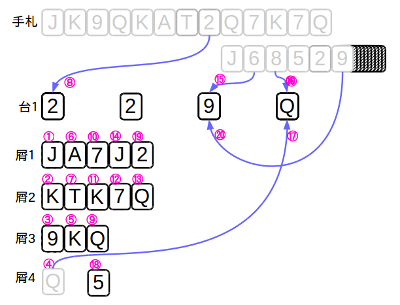
終盤と序盤の屑札を比べると、序盤に屑1〜4に載せられたカードのかなりが最後まで残っていることが分かるだろう。つまり、序盤にしっかり考えて、最後にするすると全て取り出せるように、あるいは取り出せる可能性が高くなるようにどの屑札の上に重ねるかが「計算」の成功率を上げる鍵となる。
野崎昭弘氏の「とらんぷ」に成功率を上げる戦略があったので、紹介しておく。
Kは適当に置くとその下のカードが死んでしまうので、K用の屑札の山を確保しておく。
台札に早く付けられるカードと遅くでないと付けられないカードがある。Aは遅め、Qは2枚が早く残り2枚は遅い、Jはだいたい遅い。この早い遅いを考慮し、早いカード用の屑札の山、遅いカード用の屑札の山を決めておく。
で、そのあとは、上の図で示したように、逆順に繋がるように工夫してどの屑札の山に置くかを決める。その場で直ぐにはつながらないことが多く、今後出てくるカードのことを考えて、後から繋がったり、あるいは台札に出すことも考えて、要するにあらゆる可能性を考えると成功率は上がっていく。
成功率であるが、普通にやる程度ではなかなか50%に達しないと思う。屑札上の繋がりをきちんとメモしながら熟達してくると、8割は行くであろう。
ところで、コンピュータを使って、しっかり調べてプレイすればどこまで成功率が上がるのであろうか。
こういうことは、ネットで調べると直ぐに結果が得られる。便利な時代だ。
カルキュレーション(Wikipedia)
田中哲朗:『部分ゲームの解析結果を用いたカルキュレーションの戦略』情報処理学会論文誌、3064-3073
田中氏といえばGPS将棋の人というイメージだが、実際にはゲーム情報学の専門家で、幅広い研究で知られている。
計算の成功率は、田中氏の論文によると、99%を確実に超えるようである。
論文をしっかり読んだ訳ではないのだが、いろいろ頑張って高い成功率を達成したようだ。
しかし、今回のモンテカルロ木探索を使った実験とは方針が相容れないので、こういう努力は今回は排除する。
あくまでも、ほとんど成功しない超バカなプログラムを用意し、それをモンテカルロ木探索と組み合わせるとそこそこ高い成功率を出せることを検証する。
計算のバリエーション:
コンピュータ:台札のA,2,3,4は最初から出さず、手札から出てきたときに出す。直ぐに台札に出さなくてもよい。他は計算と同じ。
超人:屑札の山を3つにしたもの。他は計算と同じ。
いずれも、計算よりも難しくなる。とくに超人は難しくなり、本当に超人向きになる。
次回は、ほとんど成功しない馬鹿なプレイヤー・プレイヤについて説明する。



