モンテカルロ木探索で一人不完全情報ゲーム「計算」を賢くする[7]

モンテカルロ木探索では、いわゆる「木」を用いる。木は、ノードの集まりで、親子関係があり、１つのノードに対して複数の子ノードがぶら下がる。

まず、用意したNodeクラスを見てみよう。

class Node {
  Node    parent = null;      // 親

  boolean　childmovetype;    // true: 札移動タイプ false:手札オープン
  Node    children[] = null;  // 子ノードはまとめて作られる
  int    childcnt = 0;       // 子ノードの個数

  Move    move = null;        // 手

  int    playcount = 0;      // このノードを起点にplayoutした回数

  double    successsum = 0.0;   // 成功合計
  double    success = 0.0;      // 成功率　= successsum / playcount
}

ノードは、カードに対して操作をすることにより盤面が変化する度に作られるのだが、盤面情報自体は含んでいない。これは、盤面の状態はカードの動きを木の枝にそって順番にたどることで確実に求められるので、ノード自身には盤面状態を保持しない。
ノード自身はそれほどメモリを食わないが、盤面データは「計算」という規模の小さなゲームでもそこそこ食ってしまう。もし、盤面データがノード毎に用意されていると、メモリの大部分は盤面ということになる。盤面を保持していること自体、とくにメリットはないので、Nodeの要素には入れていない。

ノードには、カードの移動に伴ってできたものと、カード(手札)をめくってできた2種類があり、この２つのノードを区別しなければいけない。
どうしても2種類のノードをきちんと区別したい（行儀よくやりたい）場合には、Nodeを継承したMoveNodeとOpenNodeというクラスを作ると良いのだが、ここではこのまま話を進める。

ここでは、Node自身のノードタイプではなく、子ノードのタイプをchildmovetypeに保持している。
子ノードはない場合もあり、1個以上の場合がある。子ノードへのリンクの配列と、子ノードの個数を持っている。 Javaでは、配列のサイズを別に保持する必要はないのだが、特殊な使い方をするため、わざわざ子ノードの個数を保持している。子ノードの個数はないプログラムも可能なのだが、そのままにしておく。

子ノードがカードの移動のとき、getAllMoves()で与えられる全ての移動に対する子ノードを用意する。このときは、子ノードの配列には全ての移動に対して１つずつノードが生成され、子ノードの個数(＝全ての移動の個数)も保持する。

子ノードが手札をめくるとき、表になったカードの数字を配列の添字として使うと楽になるので、常に要素数13+1の配列を用意し、残り手札の中にある数字に対してだけノードを用意する。このときの子ノードは、残り手札を見て一気に作るのではなくて、モンテカルロ木の成長過程で、手札をめくった時に必要なら子ノードを作る。
早めにちゃんと準備するのではなく、必要になったときに初めてつくるというとても怠惰な方式を選んでいる。いわゆるlazyな方法を選んでいるのだが、これは木が無駄に大きくならないようにするためである。実際に対応するコードが出た時に再度説明を加えよう。

moveという移動内容を示すMoveオブジェクトを保持している。このmoveに対応する移動を行った結果、現在のノードができたということを示す。

モンテカルロ木探索なので、プレイアウトの回数を保持している。詳しい説明は後述する。プレイアウトしたときの成功／失敗に関するデータを保持するため、successsumとsuccessが存在する。successsumは、計算の都合で入っている補助的なものである。
モンテカルロ木探索でとても重要なのが成功率successであるが、詳細はプログラムコードとともに徐々に説明していく。

ノード間の関係は次図のようになる。○はノードを示し、□はノードの中の移動(Move)を示している

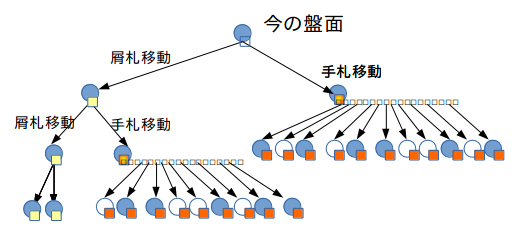
手札移動を行うと、手札のトップの札がなくなるので、まだ手札が存在するかぎり手札を1枚めくらないといけない。そのとき、一気に子ノードがいっぱいできている。 この木を管理するためのコードを書き加え、さらに木の一番下の端ノード（葉ノード）それぞれでプレイアウトを行うとモンテカルロ木探索が行われる。

Nodeクラスのメンバーを示したが、つぎにコンストラクタを考えよう。

引数なしのデフォルトと、親ノードとカード移動を与える場合の２つのコンストラクタを用意した。

Node( Node pr, Move mv ) {
  parent = pr;
  ++parent.childcnt;
  move = mv;
}

Node() {
}

さて、モンテカルロ木をプレイアウトしながら成長させることで、次の最善手を見つけようというのがモンテカルロ木探索である。

最初は、原始モンテカルロ木探索と同じで、ルートの直下に次に可能な手に対応したノードを生成し、各ノードに対してプレイアウトをどんどんやっていく。このとき、各ノードで行うプレイアウトの上限値（閾値）を決めておき、それを超えるとそのノードのプレイアウト結果は捨てて、下位のノードを作ってそちらに対してプレイアウトを行う。こうすると、もとのノードにはプレイアウトがなくなったが、その下位ノードのプレイアウト回数の合計は１回増えることになる。

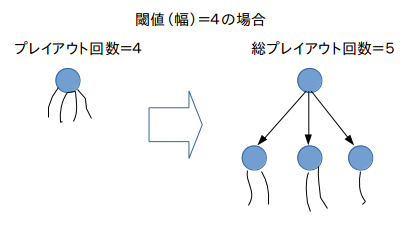
プレイアウト回数をどんどん増加していくと、閾値を超えるノードができることで下位ノードを作ることになり、これで木が成長していく。
つまり、プレイアウトする毎に木を成長させるので、原始モンテカルロの場合と違い、木の成長を意識したプレイアウトメソッドを用意しないといけない。

void playouttree( Node node )

ノードを与えて、そのノードで示される部分木に対してプレイアウトを１回追加することを行うことになるが、この説明がモンテカルロ木探索の最も重要な部分になり、とても長くなるので、次回以降で説明する。