モンテカルロ木探索で一人不完全情報ゲーム「計算」を賢くする[14]

まず最初に、プレイアウト回数を１００万回にした場合の結果を示す。

    プレイアウト回数=１００万、UCB定数=0.5, 閾値=5 で　94/100

プレイアウト回数を増やすと、成功率が着々と上昇し、９０％を超えることができた。
といっても、たった１００回しかゲームが行われていないので、甚だ精度が心もとない。本当なら１万ゲームくらいやり成功率を求めるべきなのだが、時間がかかるのでやめた。
それでも、１００万回やれば成功率は９割を超えると言えるだろう。

さて、今回は、いままでのパラメータとは違う種類のパラメータをでっちあげ、有効性を調べてみよう。
プレイアウトが終わったときの２つの場合を示すので、この差について考えてみよう。

Hand:     _ : 
Table:  K  K  7(T)  K 
[1]  
[2]  
[3]  
[4]  TK

Hand:     _ : 
Table:  6(7)  9(J)  2(5)  7(J) 
[1]  JJAJ65K
[2]  AJ7T8
[3]  4TKK795T8
[4]  2K9Q

現状では、プレイアウトの結果の成功率の値は、1.0(成功) と0.0(失敗)しかない。 この事について考えてみる。

上の２つの場合、屑札として残ったカード枚数は、2枚と２５枚である。一方は、成功まであと一歩の状態であるが、もう一方はどうにもならない大失敗である。この差をなんとかしようというのが今回のテーマである。
プレイアウトが終わったとき、屑札の山に１枚でも少ないほうが成功に近いと考えてみよう。

残り枚数１はありえない。理由の説明は省略するの、考えて欲しい。

それで、残り枚数に応じて成功率が変わるグラフを作ってみた。左側は従来のもので、右側が今回考えたものである。

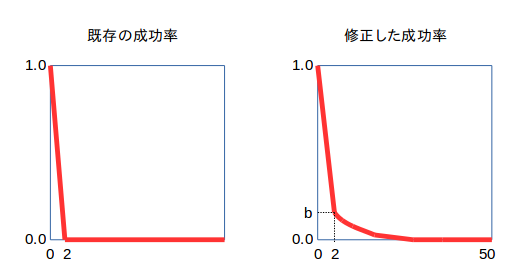
残り枚数が２枚、１０枚、２０枚となった場合、これら３つの状態の成功率をどれも0.0にするのではなく、それぞれ0.2, 0.05, 0.02 とかにできないであろうか。
それで、右グラフのような結果を出すメソッドを用意した。引数として、残り枚数を与えると、それに応じた妥当な成功率を返してくる。

グラフ中の縦軸のbは、残り枚数が２枚の時の成功率で、プログラム中ではBADMAXとなっている。

// 残り札数から成功率を見積もる
  double    resttoSuccessRate( int r ) {
    if( r <= 1 )
      return    1.0;
    int failnum = (int)(MAXCOUNT*0.5);
    if( r > failnum )
      return    0.0;
    double sc = (1.0-(double)(r-2)/failnum);
    sc = BADMAX * sc * sc;
    return    sc;
  }

計算は相当いい加減にしているが、右図のような傾向があれば良い。もっと頑張りたい人は、自分で工夫して、素晴らしい結果になったら、ぜひ教えて欲しい。

このメソッドを simpleplayoutの最後で呼び出すようにすれば、修正はおしまいである。

double    simpleplayout() {

    for(;;) {
      opentefuda();        //  手札をめくる

      ArrayList<Move>    list  = getAllMoves();      // 札の移動を考える
      if( list.size() == 0 )
        break;

      Move    mv = selectRandomly(list);
      mv.exec();
    }

    //    return  restcount==0 ? 1.0 : 0.0;
    return    resttoSuccessRate(restcount);
  }

では、この残り枚数を考慮した成功率に変更した場合の効果について調べてみよう。

条件：プレイアウト回数=10000, UCB定数=0.5, 閾値=5, ゲーム数=100

BADMAX    成功率/100
  0.00        56
  0.01        57
  0.02        57
  0.03        55
  0.04        55
  0.05        60
  0.06        57
  0.07        58
  0.08        59
  0.09        60
  0.1        53
  0.2        54
  0.5        51

この表を見ると、BADMAXが0.05〜0.09あたりがやや成功率が高くなる傾向がみられる。
といっても、100回程度の試行では誤差の方が大きい。

さて、モンテカルロ木探索はどうだったであろうか。
UCBにより、急に成功率が上昇したのであるが、成功率を非常に高くしようとすると、かなり大変である。
UCBの有無は成功率に著しい差が出るが、その他のパラメータの影響はさほどでもない。
パラメータをごちゃごちゃイジるよりも、プレイアウト回数を増やす方が確実に成功率が上がる。
しかし、このアルゴリズムにも根本的な欠陥がある。それは、序盤がとても下手なことである。中盤以降は極めて正確に最適に近い手、成功する手を選択しているようであるが、序盤は判断するに十分な統計的データが得られないので、良い手を打てないでいる。

これの対策をしようとすると、しっかり機械学習させるとか、屑札の山のカードの連鎖具合をしっかり調べるなどを行わなければいけなくなり、モンテカルロ木探索でお手軽に賢くするという趣旨から外れてしまうので、そのあたりまでは深入りしない。 もし、そのあたりで良い結果が出たら、連絡して欲しい。うまくやれば、99％以上の成功率が出ることがわかっているのだが、なんかスマートな、lazyな方法があれば素晴らしいことである。

さて、これで終わろうかと思ったが、次回は、ここまで説明してきたモンテカルロ木探索とは違う単純な方法で高い成功率を出すことにチャレンジしてみようと思う。
そんな方法は果たしてあるのだろうか？