せっかくOctaveについて書いているのに、Octaveが得意な科学技術計算についてちょっとしか書いていない。
ということで、今回は、とつぜん偏微分方程式の数値解に挑戦してみようと思う。
物理現象を偏微分方程式で表すことはよくあるのだが、偏微分方程式をきちんと解くのはほとんど不可能である。
なので、現実には、適当な境界条件のもとで数値解を求めることになる。
とりあえず、結果を先に示そう。
2次元の熱伝導について数値解を求めてみよう。
1辺0.1m(10cm)の板の1つの辺の中央に熱が加わり、周囲の温度が下図のようになる場合について計算してみよう。
温度は、外周で300度(絶対温度、室温)、一辺の中央が1600度で、その一辺の温度分布はsinカーブになっているものとする。
高さ方向は温度になっている。
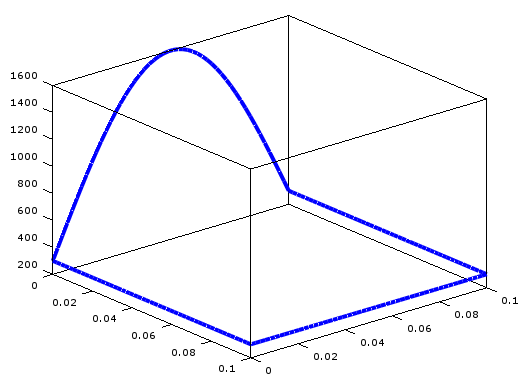 外周は上図の温度であるが、内部の温度は次の偏微分方程式にしたがって変化する。
外周は上図の温度であるが、内部の温度は次の偏微分方程式にしたがって変化する。
右辺が0になっているのは定常状態を示している。
というより、0が計算が楽なのでこれで今回は説明をしてしまう。
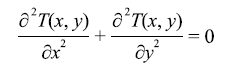
これを、正方形の板をN*Nのメッシュに切って、各点の温度を求めて図示するとこんな感じになる。
高温が赤、低温が青になっているが、これはOctaveで勝手に色づけしてくれるので便利。
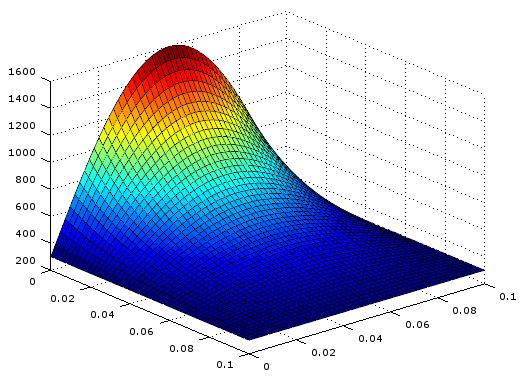
こんな図になるように計算するにはどうすれば良いのだろうか。
この図は、N=50の場合の計算結果である。
実際には、物体は3次元空間に存在するのだから、x,y だけでなく、zも加えて、N*N*Nのメッシュに切って計算するべきなのだが、こうなると点の数が非常に増えて困ることになる。
点の数は、2次元の場合で N*N、3次元の場合に N*N*N になるから大変なのだ。
いや、本当は次元が増えるというのはそんなに甘いものではない。もっと急激にデータ爆発が起きるのだが、そのあたりは次で説明しよう。
ということで、今回は、とつぜん偏微分方程式の数値解に挑戦してみようと思う。
物理現象を偏微分方程式で表すことはよくあるのだが、偏微分方程式をきちんと解くのはほとんど不可能である。
なので、現実には、適当な境界条件のもとで数値解を求めることになる。
とりあえず、結果を先に示そう。
2次元の熱伝導について数値解を求めてみよう。
1辺0.1m(10cm)の板の1つの辺の中央に熱が加わり、周囲の温度が下図のようになる場合について計算してみよう。
温度は、外周で300度(絶対温度、室温)、一辺の中央が1600度で、その一辺の温度分布はsinカーブになっているものとする。
高さ方向は温度になっている。
 外周は上図の温度であるが、内部の温度は次の偏微分方程式にしたがって変化する。
外周は上図の温度であるが、内部の温度は次の偏微分方程式にしたがって変化する。右辺が0になっているのは定常状態を示している。
というより、0が計算が楽なのでこれで今回は説明をしてしまう。
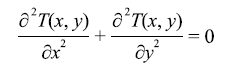
これを、正方形の板をN*Nのメッシュに切って、各点の温度を求めて図示するとこんな感じになる。
高温が赤、低温が青になっているが、これはOctaveで勝手に色づけしてくれるので便利。

こんな図になるように計算するにはどうすれば良いのだろうか。
この図は、N=50の場合の計算結果である。
実際には、物体は3次元空間に存在するのだから、x,y だけでなく、zも加えて、N*N*Nのメッシュに切って計算するべきなのだが、こうなると点の数が非常に増えて困ることになる。
点の数は、2次元の場合で N*N、3次元の場合に N*N*N になるから大変なのだ。
いや、本当は次元が増えるというのはそんなに甘いものではない。もっと急激にデータ爆発が起きるのだが、そのあたりは次で説明しよう。



