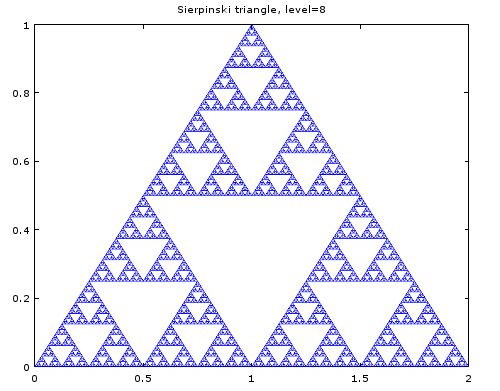
Sierpinskiの三角形は、再帰的にどんどん三角形を細かくしているように見える。
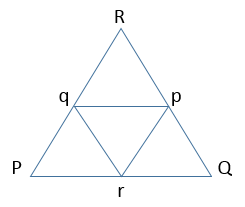
つまり、右図において、与えられた三角形PQRに対して、P、Q、Rの対辺の中点をp、q、rとしたとき、
△PRQ ⇒ △Pqr, △pQr, △pqR
という風に、3つのサイズが半分になった三角形3つを描くのを、延々と再帰的に繰り返すだけなので、とても簡単なプログラムで実現できる。
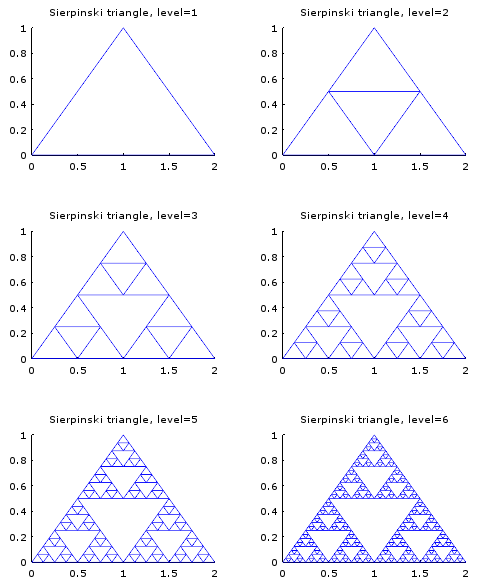
今回は、もうちょっと工夫して、1つの画面にレベルを1つずつ増やしながら描くというのをやってみた。
1;
function draw_triangle(P,Q,R,n)
n = n - 1;
if n == 0
X = [P(1),Q(1),R(1),P(1)];
Y = [P(2),Q(2),R(2),P(2)];
plot(X,Y)
else
p = (Q+R)/2;
q = (R+P)/2;
r = (P+Q)/2;
draw_triangle(P,q,r,n);
draw_triangle(p,Q,r,n);
draw_triangle(p,q,R,n);
endif
endfunction
for num=1:6
subplot(3,2,num)
hold on
draw_triangle([0,0],[2,0],[1,1],num);
hold off
title( sprintf("Sierpinski triangle, level=%d",num) );
endfor
プログラムの最初に
1;という不思議な、明らかにゴミと思われるのが入っているが、これには訳がある。
これを取り去ると、エラーが出て動かなくなる。
理由は、Octaveでは、ファンクションとスクリプトのファイルが区別されてしまうからである。
ファイルの最初に関数宣言があると、関数のファイルとみなされ、そのファイルにスクリプトを書いてしまうとエラーになってしまう。
これを避けるための方法が、最初に何の意味も無いスクリプトを書いて、このファイルはスクリプトであると思わせておいて、その後に関数を書き、関数の後ろに本来のスクリプトを書いたのである。
この程度の短いプログラムでも再帰があると関数をつかうことになる。これは、そういうときの裏技の1つである。
レベル6では、まだ綺麗というところまでいかないので、レベル8を以下に示す。