データ解析のための統計モデリング入門 一般化線形混合モデル(GLMM) 読書メモ2
2017年 05月 19日
このブログ記事は『データ解析のための統計モデリング入門』(久保拓弥 著、岩波書店)という、とても分かりやすい統計モデリングの入門書を、さらに分かりやすくするために読書メモをまとめたものです。
今回は第7章、一般化線形混合モデル(GLMM)についてのまとめの二回目です。
この章では複数の分布を混ぜて使う、一般化線形混合モデルついて説明がされています。
まずはロジスティック回帰にパラメータを追加したモデルについて説明されています。
このモデルでは、リンク関数に新しいパラメータが追加されて、そのパラメータは正規分布から生成されます。
なので、いろいろなパラメータについて、その値をプロットしてくれるコードを用意しました。
コードはRで書きました。
linkFunction <- function(b1, b2) {
function(x, r) {
1 / (1 + exp(-b1 - b2 * x - r))
}
}
xl <- "x"
yl <- "q"
xs <- runif(100, 0, 10)
ys <- function(r) {
linkFunction(-0.5, 0.3)(xs, r)
}
for (sd in seq(0.1, 2.0, by = 0.1)) {
rs <- rnorm(100, mean = 0, sd = sd)
ps <- data.frame(x = xs, y = ys(rs))
title <- paste0("logit(q) = -0.5 + 0.3 * x + r, r ~ N(0, ", sd, ")")
plot(0, 0, type = "n", xlim = c(0, 10), ylim = c(0.0, 1.0), main = title, xlab = xl, ylab = yl)
points(ps, pch = 1)
}コードを実行すると図が20枚プロットされます。
横軸はリンク関数に使われている説明変数 x で、縦軸は事象の発生確率 q です。q には x の他にも、平均 0 の正規分布から生成された乱数の影響があります。
この乱数が説明変数として考慮されていない影響を表します。
例えば以下のような図がプロットされます。
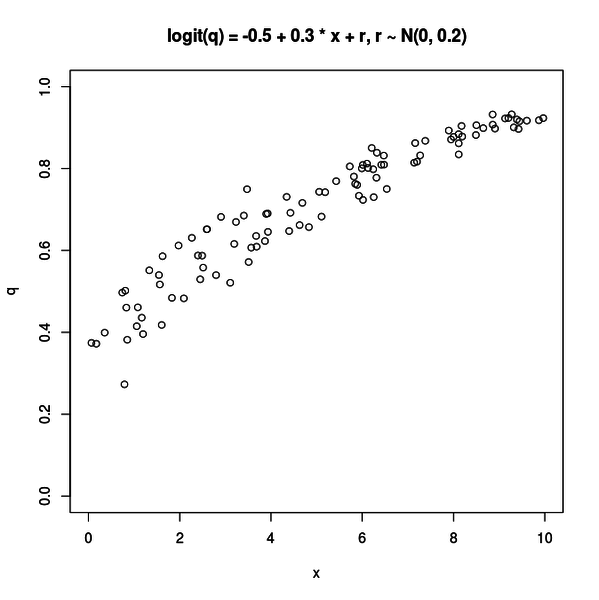
この図は分散が 0.2 の正規分布から生成された乱数がリンク関数を通して q に影響している場合です。x の増加に対して q が緩やかに上昇する傾向が見て取れます。
これは説明変数以外の要因の影響が少ない場合です。
一方、以下のような図もプロットされます。
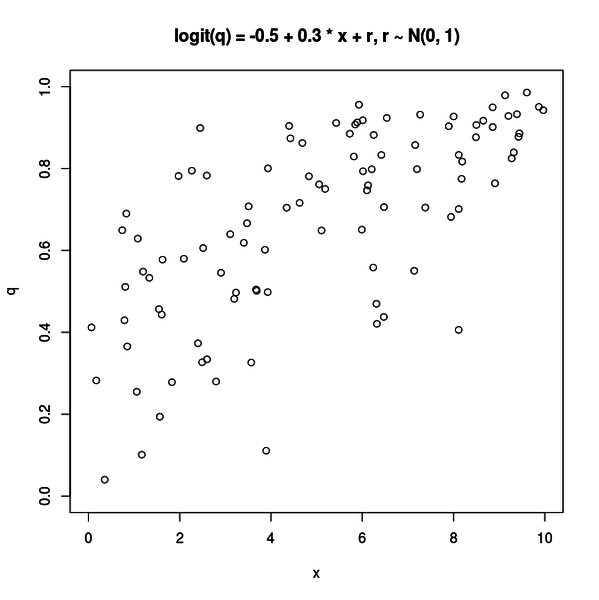
この図は分散が 1.0 の場合です。x と q の関係が分かりにくくなりました。
これは説明変数以外の要因の影響が多い場合です。
このように、パラメータを生成する正規分布の分散によって、説明変数として考慮されていない要因の影響が大きい場合や小さい場合を表現できるのが分かります。



