まだ3点が円周上にある場合しか求まっていなかった。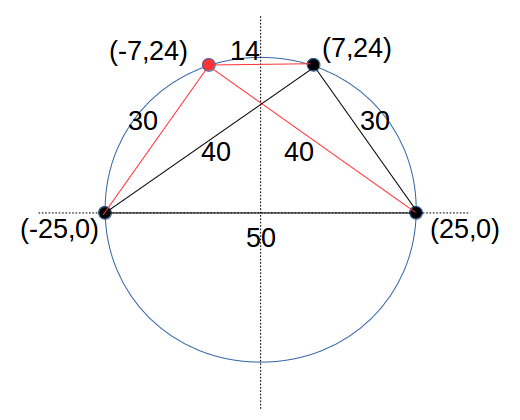
まず、3点から4点に1点だけ増やすことを考えよう。
右図のように、y軸を中心に反転した3:4:5の三角形を考えてみよう。
つまり、(-7, 24)を追加してみよう。
この点から既存の3点への距離は、30、40と14になる。
30、40の2つの距離は、図形がy軸で反転しただけであるので、以前から存在する距離でしかない。
新しく発生したのは、(-7,24)と(7,24)の距離であるが、y座標値は同じで14であることがすぐに分かる。
これで4点の場合が済んだ。
5点と6点の場合を考えよう。
 3点から4点にしたとき、y軸に対称な位置に点を取った。
3点から4点にしたとき、y軸に対称な位置に点を取った。
今度は、x軸に対象な位置に点をとってみよう。
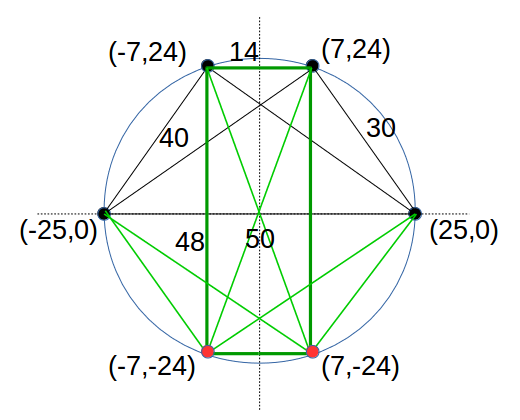
すると、6点の場合が右図のようになる。
中央に幅14、高さ48の長方形が見えている。
この4頂点は円周上の点であり、対角線は円の直径になっているので、計算するまでもなく50である。
上下反転した位置にコピーすると頂点は2点増えた。
任意の2点間の距離で、新たな距離は上下の2頂点を結ぶものだけなので、48が増えただけである。
したがって、6頂点の場合は、右図に記入されている6つの座標値が求めるものである。
さあ、もっと頂点を増やしていこう。
ここまでわかってしまえば、後はプログラムを書いて実行するのみなので、解説はこれで終える。
6点、10点、14点、18点、22点、、、、、、
の場合という感じで求めてみた。

まず、3点から4点に1点だけ増やすことを考えよう。
右図のように、y軸を中心に反転した3:4:5の三角形を考えてみよう。
つまり、(-7, 24)を追加してみよう。
この点から既存の3点への距離は、30、40と14になる。
30、40の2つの距離は、図形がy軸で反転しただけであるので、以前から存在する距離でしかない。
新しく発生したのは、(-7,24)と(7,24)の距離であるが、y座標値は同じで14であることがすぐに分かる。
これで4点の場合が済んだ。
5点と6点の場合を考えよう。
 3点から4点にしたとき、y軸に対称な位置に点を取った。
3点から4点にしたとき、y軸に対称な位置に点を取った。今度は、x軸に対象な位置に点をとってみよう。
すると、6点の場合が右図のようになる。
中央に幅14、高さ48の長方形が見えている。
この4頂点は円周上の点であり、対角線は円の直径になっているので、計算するまでもなく50である。
上下反転した位置にコピーすると頂点は2点増えた。
任意の2点間の距離で、新たな距離は上下の2頂点を結ぶものだけなので、48が増えただけである。
したがって、6頂点の場合は、右図に記入されている6つの座標値が求めるものである。
さあ、もっと頂点を増やしていこう。

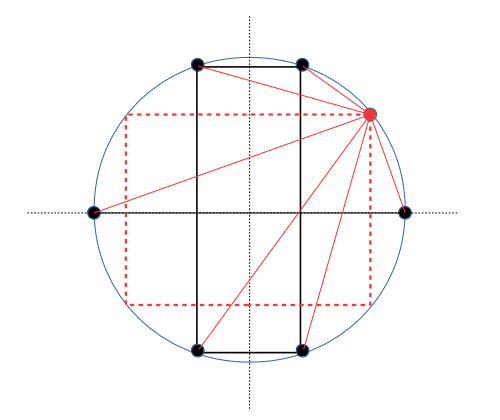
6頂点に新たな点を加えることを考えよう。
6頂点の場合、内接する4辺がx軸y軸に平行な長方形を考えるとうまくいった。
だから、7点を考える場合も、同様の長方形を考えよう。(右図)
新たな点を加えるとき、その点(x,y)の座標値は整数だけとしよう。
新たな点を加えるときに発生する新たな距離は、赤の点と、既存の黒い6点との距離だけであり、この6つの距離が全て整数であればよい。
そして、赤い破線の長方形に関しては、4辺と対角線の長さはすべて整数となる。
これにより、7点目がOKであれば、赤い破線の頂点全てを加えた6+4=10点に関しても全ての2点間距離が整数となる。
ここまでわかってしまえば、後はプログラムを書いて実行するのみなので、解説はこれで終える。
6点、10点、14点、18点、22点、、、、、、
の場合という感じで求めてみた。
(25,0) (-25,0) (7,24) (-7,24) (-7,-24) (7,-24) (625,0) (-625,0) (175,600) (-175,600) (-175,-600) (175,-600) (527,336) (-527,336) (-527,-336) (527,-336) (4225,0) (-4225,0) (1183,4056) (-1183,4056) (-1183,-4056) (1183,-4056) (3713,2016) (-3713,2016) (-3713,-2016) (3713,-2016) (2047,3696) (-2047,3696) (-2047,-3696) (2047,-3696) (7225,0) (-7225,0) (2023,6936) (-2023,6936) (-2023,-6936) (2023,-6936) (6887,2184) (-6887,2184) (-6887,-2184) (6887,-2184) (4025,6000) (-4025,6000) (-4025,-6000) (4025,-6000) (4633,5544) (-4633,5544) (-4633,-5544) (4633,-5544)
円の半径が、25→625→4225→7225とぐんぐん大きくなっている。
18点はできたが、次の22点がいつまでたっても求まらない。 なぜだろう? この方針ではいけなかったのだろうか?
18点はできたが、次の22点がいつまでたっても求まらない。 なぜだろう? この方針ではいけなかったのだろうか?



