複数人巡回セールスマン問題

2人での巡回セールスマン問題は、以下のように考えると、できる。

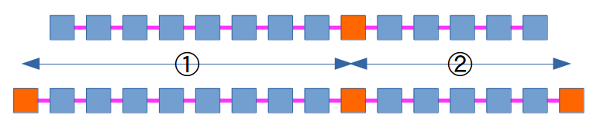
上は、両端がない循環しない紐状のルートの場合である。
これの両端の２つの街の間の距離も加え、全体でリング状になるとしたのが一般的な巡回セールスマン問題である。

ここでは、その下側のように、両端にベース（基地）を加えたものを考え、それらの間の距離も考えることにする。
すると、①がセールスマン１の巡回路になり、②がセールスマン②の巡回路になる。

これで、二人のセールスマンの巡回路が決まるので、その長さを求め、最小化すべきものを計算することで、いままでと同様に遺伝的アルゴリズムにより、二人巡回セールスマン問題が解ける。

これが分かれば、次のように考えると３人巡回セールスマン問題も解ける。

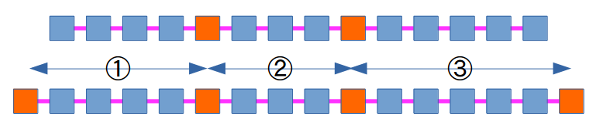
３人の場合には、両端のない経路を考える時点で、既にベース（基地）が２つ入っている。

この場合、単にベースを２つ、その他の街を１つずつの並べ替えを考えれば良いだけである。

適当に並べたときに、ベースが連続する場合があり、その場合、全くなにもしない移動距離ゼロのセールスマンが発生する訳だが、その場合にはサラリーマン間の移動距離の差が大きくなるので、そのようなケースは自動的に排除されるので、何も問題ない。

このようにして、複数人で手分けをして回る場合の巡回セールスマン問題で、公平で合理的なルートを求めることができるのである。

この他にも、さまざまな条件の巡回セールスマン問題があるので、詳しくは各自で調べてみよう。

いや、自分で勝手にさまざまな条件をでっち上げて、考えてみるのも良いだろう。