今回から、フラクタル画像を作る話をする。
幾何学的に作るのではコッホ曲線が有名だろうか。
自然界のフラクタルとしては、ブロッコリーが見事だ。
だが、ここでは、コンピュータでガンガン計算することでフラクタル画像を作ってみよう。
実は、ここで紹介する方法は、基本的にはO’Reillyから出ている「Cython」の最後の方で紹介されているプログラムをベースにしている。
フラクタル図形とは、部分と全体が一致する図形のことである。部分を拡大していくと、また同じ風景が出てきて、それをさらに拡大してもまた同様の風景が出てくる図形のことである。
言葉で説明しても分かりづらいので、まず実際にプログラムで生成されたフラクタル図形を示す。縦横1000×1000の画像を生成した。
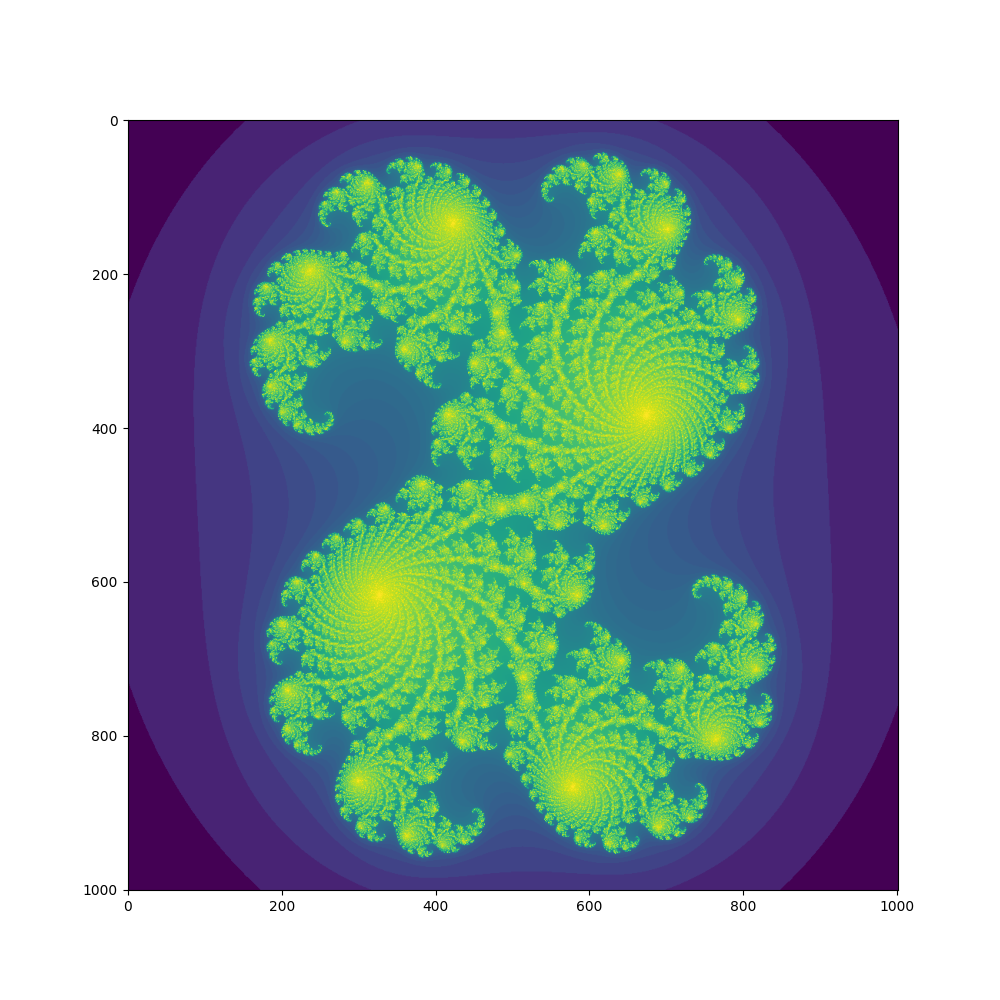
この画像は、部分を拡大すると、また同じような形がでてきて、拡大を延々と続けてもやはり同様の形が現れるというフラクタルの性質を持っている。
今回は、Pythonだけをつかって、この図形がどうやって作られているかを説明する。
複素数を使っているのだが、複素数と言っても高校数学の範囲さえ分かれば充分である。
この図形を生成するのに、複素数を利用するのだが、その式は、次の簡単な関数である。
f(z) = z*z+cなお、zとcは複素数である。
この2次式で、複素平面上の点zに対して、f(z)を求め、あらたなzとする。
cは定数であるが、複素数の適当に決められた定数である。
すると、z0→z1→z2→・・・ と延々と計算できる。
これで、与えられた複素定数cに対して、複素平面上の任意の点(複素数)に対してこの無限数列を延々と計算できる。
これを実験する簡単なプログラムを書いてみた。
c:0.322-0.047i, z0 = 0.386+0.626i
で計算を開始し、とりあえず400項まで計算してみた。
そして、数列の値を複素平面上にプロットしてみた。
表示範囲は、実部が-2から+2、虚部が-2iから+2iとしている。
import math
import matplotlib.pyplot as plt
plt.xlim(-2,2)
plt.ylim(-2,2)
c = 0.322 -0.047j
z = 0.386 + 0.626j
for j in range(400):
z = z * z + c
print(j,f'{z:+.3f}')
plt.plot(z.real,z.imag,marker='.')
plt.show()$ python3 complex_seq.py
0 +0.079+0.436j
1 +0.138+0.022j
2 +0.341-0.041j
3 +0.436-0.075j
4 +0.507-0.112j
5 +0.566-0.161j
・・・・・・
中略
・・・・・・
395 +0.631-0.067j
396 +0.715-0.132j
397 +0.816-0.235j
398 +0.933-0.431j
399 +1.007-0.851j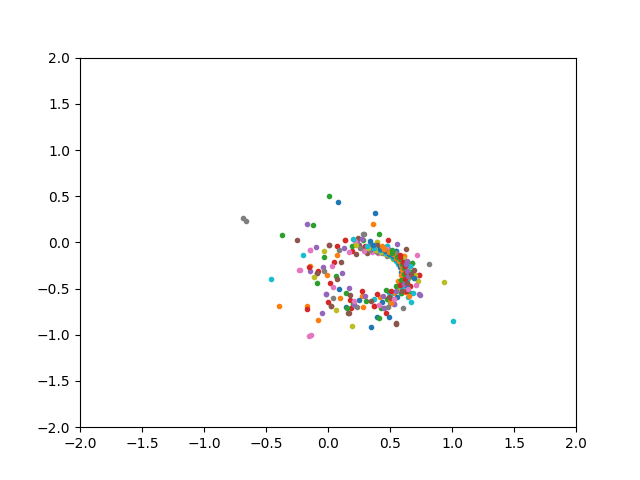
400項まで計算しても発散はせず、ぐるぐると回っている感じ。
これは、特定の点zに対して延々と級数を計算したのだが、多くの場合発散してしまう。
それで、絶対値が2以上になったら発散とみなし、その時の項数を初期の点に対する値J(z)とする。全然発散しないこともあるので、計算する最大の項数(n_max,繰り返し数)を決めておき、それに達したらJ(z)=n_maxとする。
関数 J(z)は、zの値に対して非負整数となる。この値に対して色付けすると何らかの模様が出てくるかも知れない。
以上の説明に従ってJulia集合の絵を生成するPythonのプログラムを次に示す。
## Julia集合
## matplotlib.pyplot での出力。
import numpy as np
import matplotlib.pyplot as plt
import time
def escape(z,c,z_max,n_max):
i = 0
z_max2 = z_max * z_max
while norm2(z) < z_max2 and i < n_max:
z = z * z + c
i += 1
return i
def norm2(z):
return z.real * z.real + z.imag * z.imag
def calc_julia( resolution, c, bound=1.2, z_max=2.0, n_max=1000 ):
step = 2.0 * bound / resolution
counts = np.zeros((resolution+1,resolution+1), dtype=np.int32)
for i in range(resolution+1):
imag = bound - i * step
for j in range(resolution+1):
real = -bound + j * step
z = real + imag *1j
counts[i,j] = escape(z,c,z_max,n_max)
return np.asarray(counts)
def julia():
tm_start = time.time()
jl = calc_julia(1000,(0.322+0.047j))
tm_end = time.time()
plt.figure(figsize=(10,10))
plt.imshow(np.log(jl))
print("time={}".format(tm_end-tm_start))
plt.show()
if __name__ == '__main__':
julia()$ python3 julia_py.py
time=25.323479175567627実行すると、最初に示したフラクタルな画像が、matplotlibにて表示される。
表示範囲は、実部が-1.2から+1.2、虚部が-1.2iから+1.2iとしている。
1001×1001の配列を用意し、表示範囲に対応させいて、各点に対して求めた発散までの回数を記録する。
‘__main__’ 以下で実際の画像表示を行っているが、発散までの回数の対数に対して、デフォルトのカラーマップ(ヒートマップ)による色付けがなされている。多くの場合、対数にしてから評価すると性質がはっきり分かることがあるので、ここでも対数を利用している。
図にする部分は、matplotlib.pyplotを使っているが、詳細な説明は省略するので、詳しく知りたい場合にはmatplotlibのマニュアルを参照されたい。
次回から、このPythonのプログラムをCythonに変えていこう。
Pythonのままでは、25秒以上かかっているが、どのくらいまで速くなるだろうか。




