Cython(17) Mandelbrot集合

次のようなフラクタル画像の方が、Julia集合よりもよく知られていると思う。
これが、Mandelbrot(マンデルブロ)集合で、作り方はJulia集合とほとんど同じであり、プログラム上でも、僅かの差しかないので、その話をしようと思う。

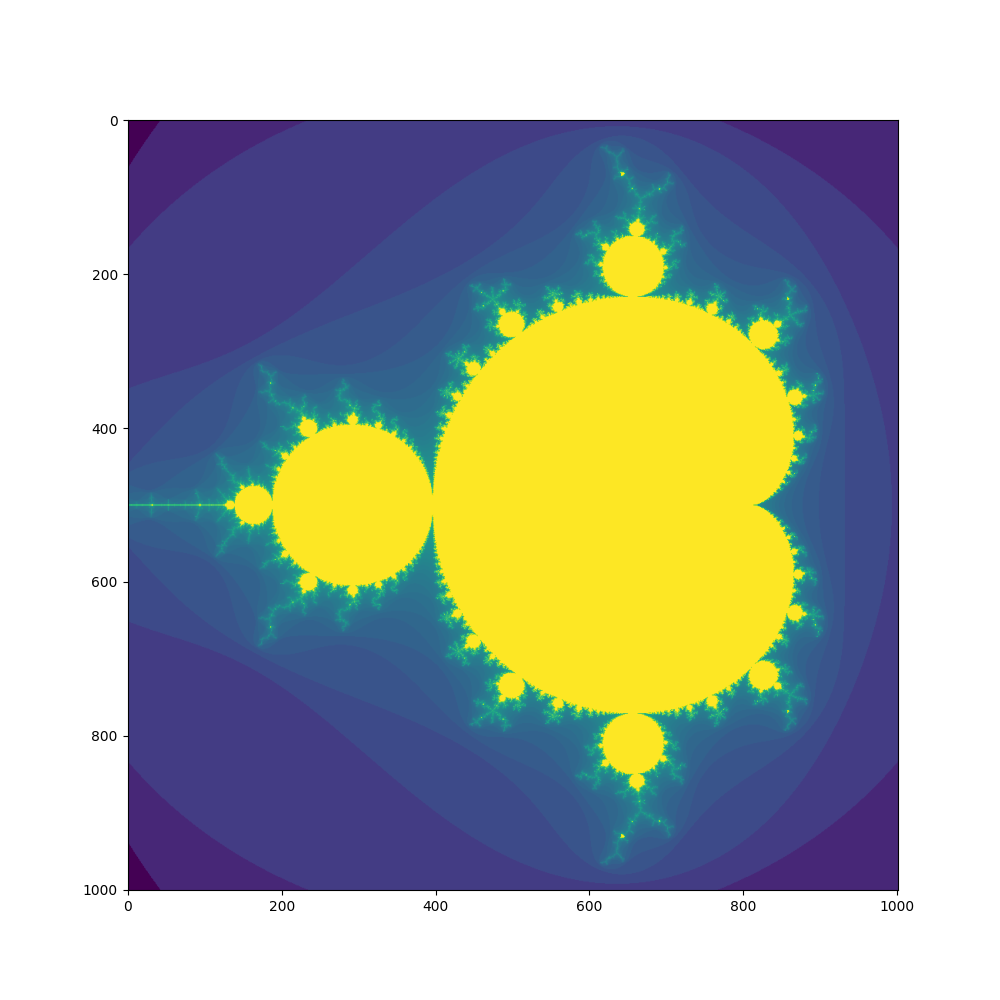
今回は直接Cythonとは関係ない話になってしまう。
専門用語では、複素力学系と呼ばれている分野で、書籍も何冊か出ているようである。
ここでは、複素力学系についてはあまり触れず、Julia集合とMandelbrot集合が姉妹関係にあることと、複素関数をちょっと変えて別の図を作れることを紹介する。
ということで、複素関数などの知識は特に必要としないので、安心して大丈夫。

Julia集合でも、Mandelbrot集合でも、次の複素数を求める関数は

z = z * z + c

を使う。したがって、発散するかどうかを延々と調べる関数escapeはそのまま使える。

cdef int escape( double complex z, double complex c,
        	double z_max, int n_max) nogil:
	cdef:
    	int i = 0
    	double z_max2 = z_max * z_max
   	 
	while norm2(z) < z_max2 and i < n_max:
    	z = z * z + c
    	i += 1
	return i

そして、この関数を呼び出す部分が関数 def calc_julia( int resolution, double complex c, … ) の中にあって、

counts[i,j] = escape(z,c,z_max,n_max)

となっているのだが、この1行だけを変更するとJulia集合がMandelbrot集合になる。
zは複素平面上の点で、求めたい場所を与えるので、そのままとする。
cが適当に与えた定数で、複素平面上のどの点についても固定の値だった。
cは２乗後に加えているので、オフセットのようなものである。

Mandelbrot集合では、cの代わりにｚを与える。
つまり、ｚを延々と繰り返し計算するのだが、ｚを順にz0,z1,.. と書くことにすると、

z1 = z0*z0 + z0
z2 = z1*z1 + z0
z3 = z1*z1 + z0
………………

という風に計算が進む。
これにより、場所によって、cが変わることになり、結局Mandelbrot 集合が出来上がる。

非常に僅かな変更でできてしまうので、プログラムは省略する。
違う部分は、次の1行でしかない。

counts[i,j] = escape(z,z,z_max,n_max)

Mandelbrot集合の場合には、原点に対して対称ではなく、実軸の負の方向に伸びるので、中心を(-0.5,0)にした。

さて、これだけで終わってはつまらない。
複素数の式を適当に与えれば、何かの図ができそうな気がする。
複素数列を求める式（漸化式）を次のようにしてみよう。n=2がMandelbrot 集合である。

z = z ** n + z0

その結果は、つぎのようになった。

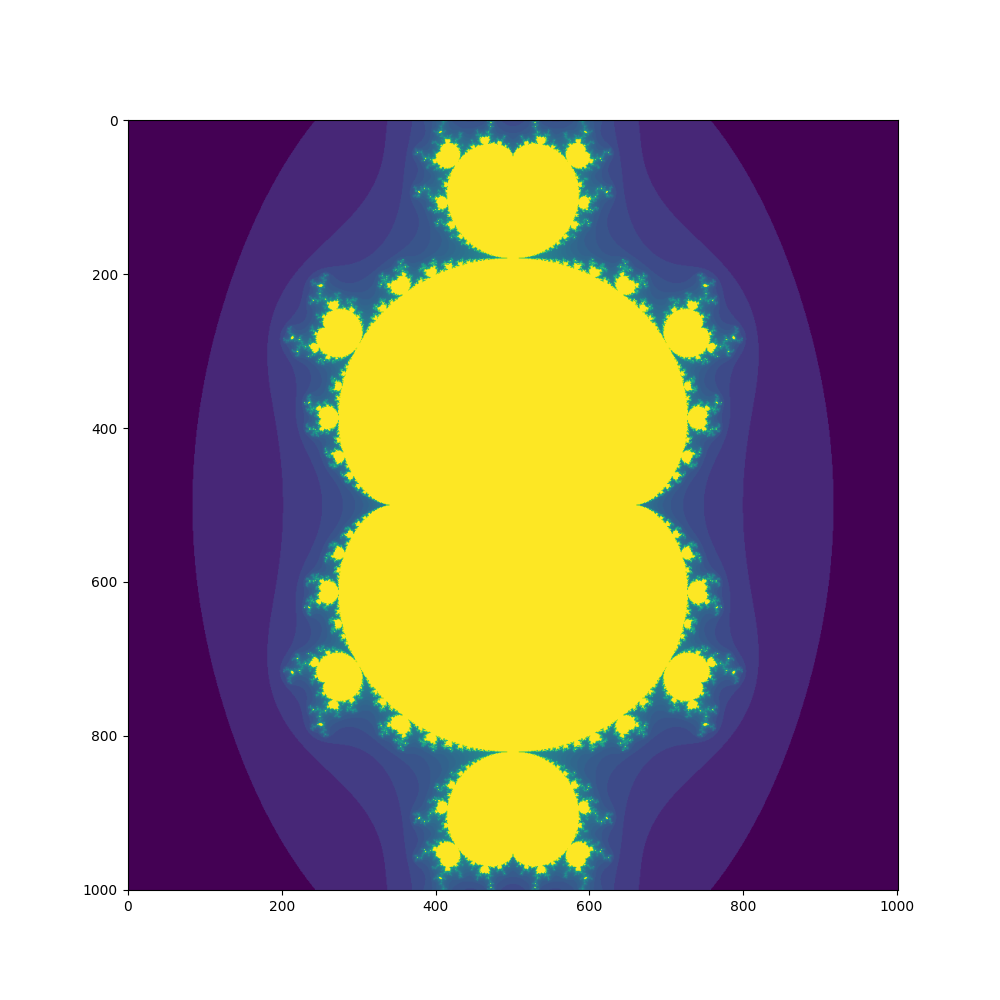
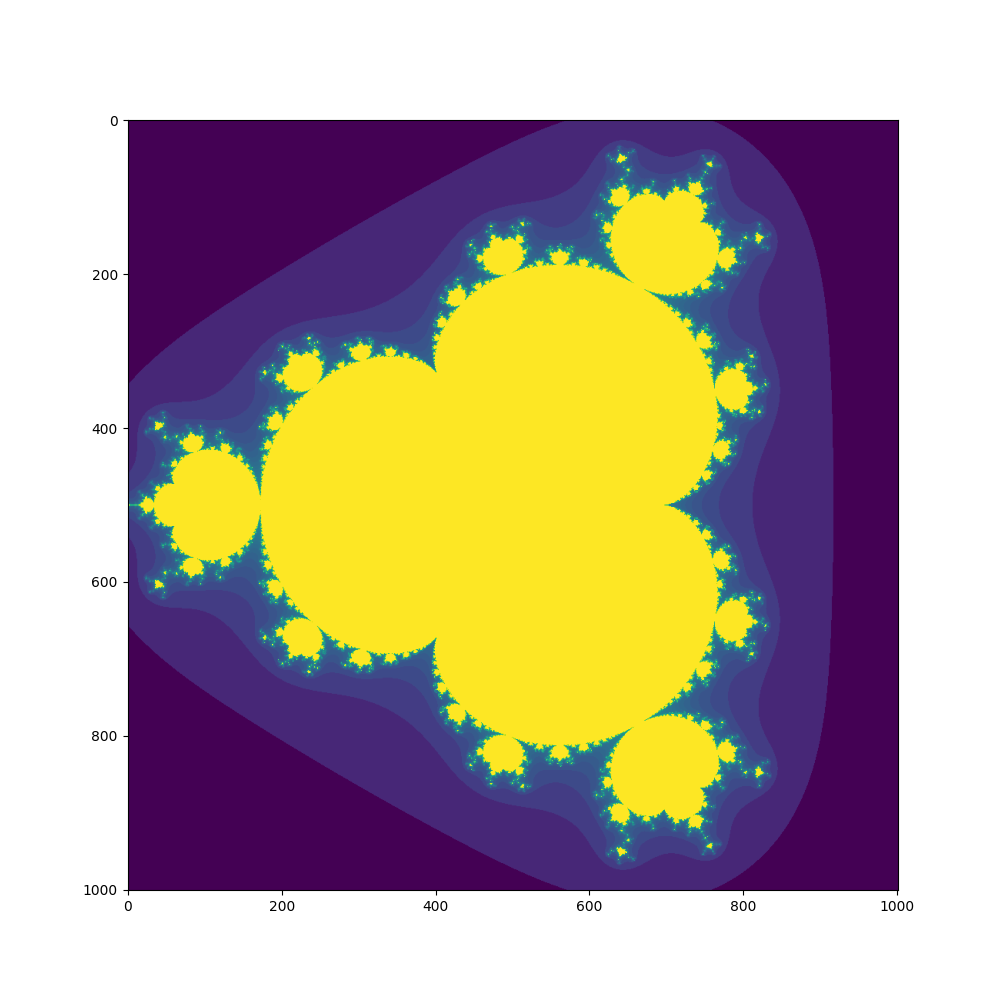
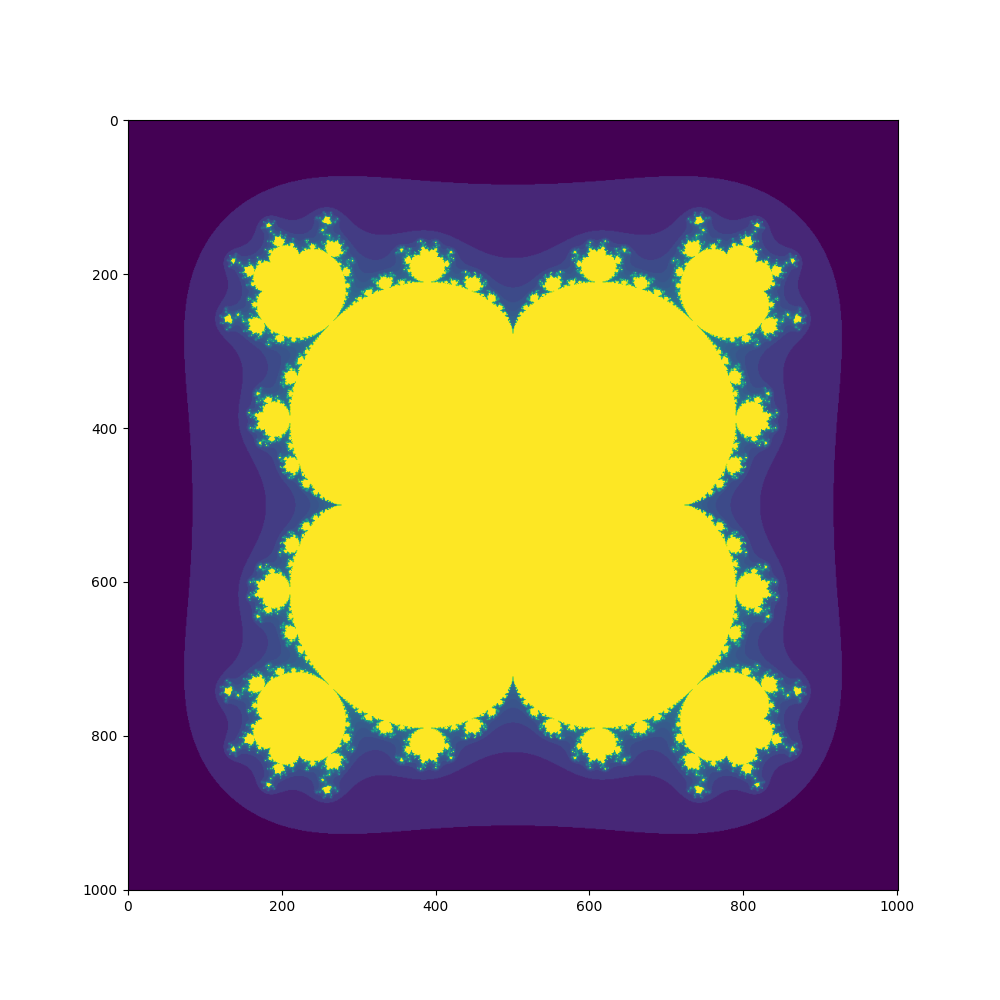
実は、このようにして複素力学系によってフラクタル画像を作る方法は1990年ころに流行し、本も何冊か出版された。今だと簡単に計算でき、動画にすることも簡単になったが、当時のコンピュータでは時間をかけてやっときれいな静止画が得られるくらいだったようだが、もう記憶が定かでない。

関数として、もっとも簡単なｎ次多項式の複素関数を示したが、なかなか発散しない複素関数なら何でもよく、さまざまな関数、例えば複素数のlogを用いた場合などの研究も行われているようであり、ネット上でいろいろ見つけることができる。

複素力学系の説明は、これで終わりとする。