進化計算学会 論文誌 論文賞を振り返る

12月18日（日）2022年度の進化計算学会 論文誌 論文賞が発表されました．
この記事では，最初に進化計算学会論文誌の紹介と今までの論文賞の振り返りをします．
そして，2022年度論文賞 受賞論文の図の再現に挑戦します．

進化計算学会論文誌

進化計算学会論文誌は，進化計算学会が発行する唯一の学術雑誌です．査読つきのオンライン学術誌(Academic journal)であり，J-STAGEで公開されています．誰でも，無料で読むことができます．
個人ページになりますが，こちらから論文リストを確認できます．
論文賞を受賞した論文は，赤字で強調表示されています．論文賞は，1年に1件のみ選出されます．

論文賞 受賞論文

今までに論文賞を受賞した論文は，以下になります．

2012年: 解の支配領域の自己制御による進化型多数目的最適化: 多数目的0/1ナップザック問題における性能検証と挙動解析
2013年: 被覆度を考慮したマルチスタート法による多目的連続関数最適化: Adaptive Weighted Aggregation
2014年: Distance-weighted Exponential Natural Evolution Strategyの提案と性能評価
2015年: 二段階の非支配ソーティングと指向性交配による制約付き多目的最適化
2016年: 大域的多峰性関数最適化のための実数値GAの枠組みBig-valley Explorerの提案
2017年: 劣個体分布に基づくDII analysisの提案と応用
2018年: 応答曲面法を用いた複数車種の同時最適化ベンチマーク問題の提案
2019年: リニアエアロスパイクエンジンの多目的設計最適化
2020年: オフィスビルにおける空調スケジュールのシミュレーションに基づく進化型多目的最適化
2021年: レプリカ交換型差分進化マルコフ連鎖による多峰性分布からの効率的なサンプリング
2022年: 推定パレートフロントに基づいて重みベクトル群を配置する多目的進化アルゴリズム

ここからは，2022年度論文賞 受賞論文に関する話をします．

2022年度 受賞論文

2022年度 論文賞を受賞した論文は，以下になります．
高木智章, 高玉圭樹, 佐藤寛之: 推定パレートフロントに基づいて重みベクトル群を配置する多目的進化アルゴリズム, 進化計算学会論文誌, 12巻, 2号, pp. 45–60, 2021.
論文はこちらから読めます．また，プログラムは個人リポジトリかPlatEMOからダウンロート出来ます．
論文は，2022年1月12日にJ-STAGEで公開されました．

2022年度 受賞論文の図の再現

2022年度 受賞論文は，利用したツールの情報が論文に明記されています．また，多目的進化アルゴリズムのプログラムも公開されています．そのため，論文に掲載されている図の再現に必要な手がかりが多数あります．論文中に99ある図の中で，今回は，図5(d)の再現方法を紹介したいと思います．

まず，MATLABの実行環境とUniformPoint.mを用意します．UniformPoint.mは，分布が均一な点群を生成するPlatEMOのUtility functionsの1つです．そして，以下のプログラムで点群を生成します．

F = UniformPoint(19,3,'ILD');
F = [
    F * 5 + repmat([10 0 0],19,1);
    F * 6 + repmat([0 9 0],19,1);
    F * 7 + repmat([0 0 8],19,1);
    ]/15;
F = F ./ repmat(sqrt(sum(F.^2,2)),1,3);

点群Fは，以下のように変化します．

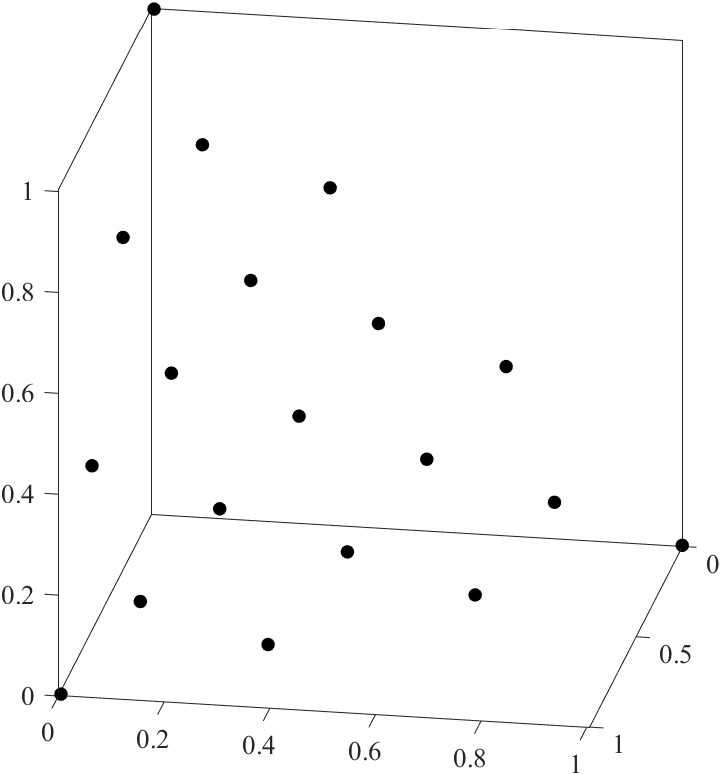
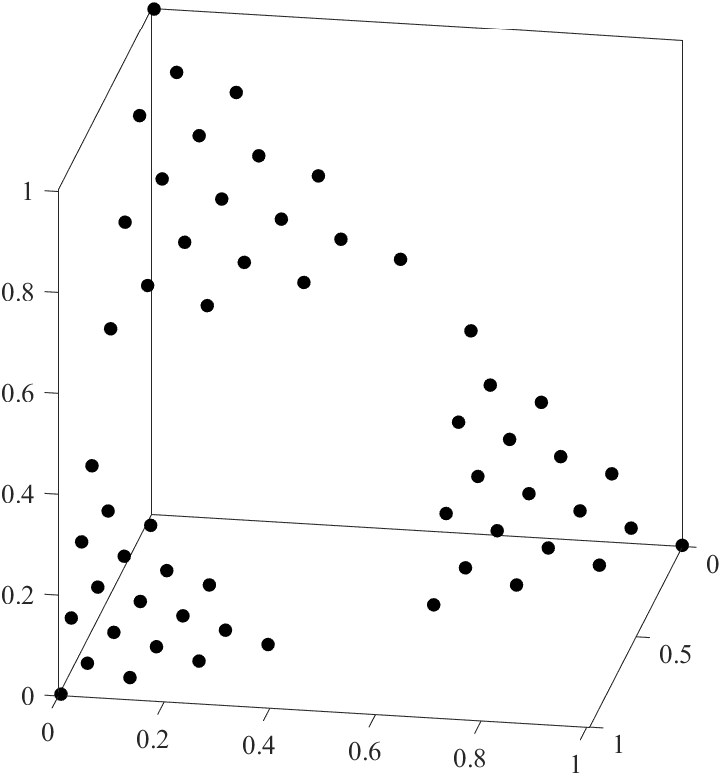
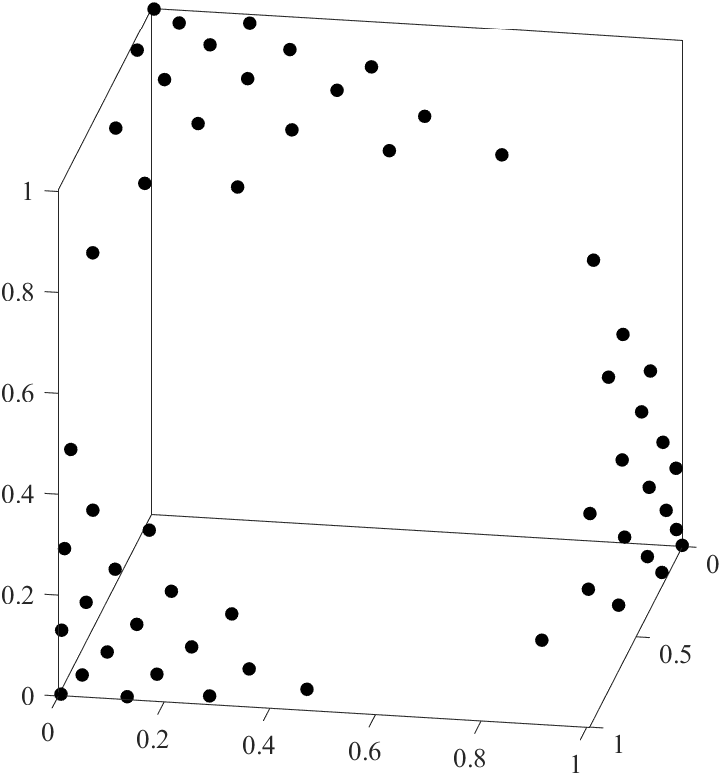
1行目は，UniformPoint.mを利用し，3次元空間の単位超平面に均一分布する19個の点からなる点群Fを生成します．2-6行目は，点群Fをコピー，変形することで，単位超平面に分布する19*3個の点からなる点群Fを生成します．7行目は，点群Fを変形することで，曲面に分布する点群Fを生成します．
真ん中の図は図3(b)と同じであり，右の図は，図3(a)と同じです．

次に，以下のプログラムで推定モデルを構築します．

Y = vecnorm(F,1,2);  % 出力Y：L1ノルム
X = F ./ Y;          % 入力X：L1単位ベクトル
net = newrbe(X',Y'); % 応答曲面法RBNN

ここで，出力Y：L1ノルムは，スカラー値の集合です．入力X：L1単位ベクトルは，単位超平面に分布する点群であり，上の2-6行目の図と同じです．netは，構築した推定モデルです．newrbeはMATLABの組み込み関数であり，こちらに公式情報があります．

そして，以下のプログラムで推定パレートフロントを獲得できます．

Xtest = UniformPoint(4960,3,'ILD');
Yhat = sim(net,Xtest')';
Fhat = Xtest.*Yhat;

点群Xtestと点群Fhat(+点群F)は，以下になります．

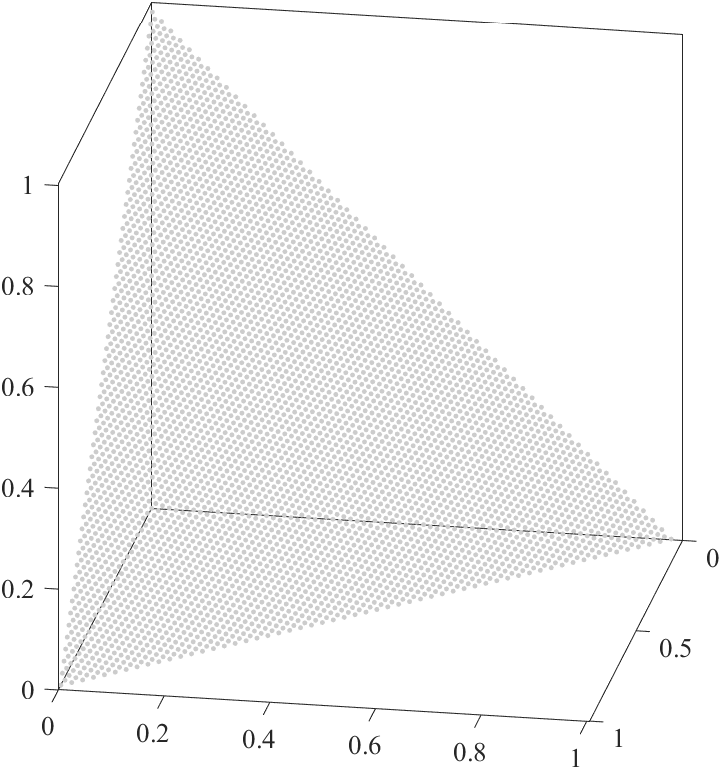
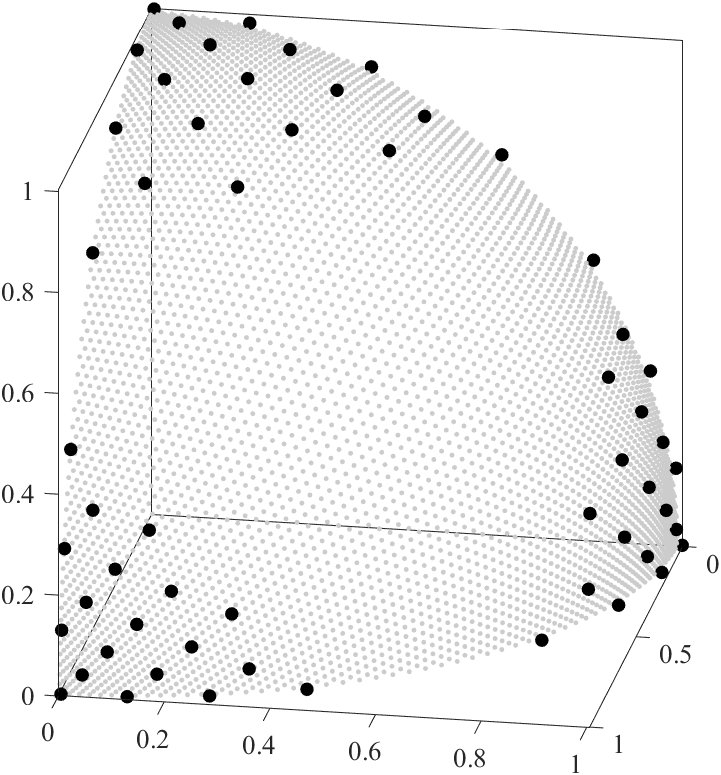
Xtestは，推定モデルへの入力点群です．自分のPC環境では，Xtestの点の数を3万点以上にするとメモリエラーが出ます．入力点群は，均一でなくとも構いません．ここでは分かり易さのため，およそ5千点からなる単位超平面に均一分布する点群を利用します．
Yhatは，Xtestに対応する，L1ノルムの推定値の集合です．Fhatは，推定パレートフロントを表す推定目的ベクトル群になります．右の図は，図5(a)$\alpha=0.40$と同じ図です．

上記プログラム推定パレートフロントの獲得において，点群Xtestを変更することで図5(d)を再現できます．
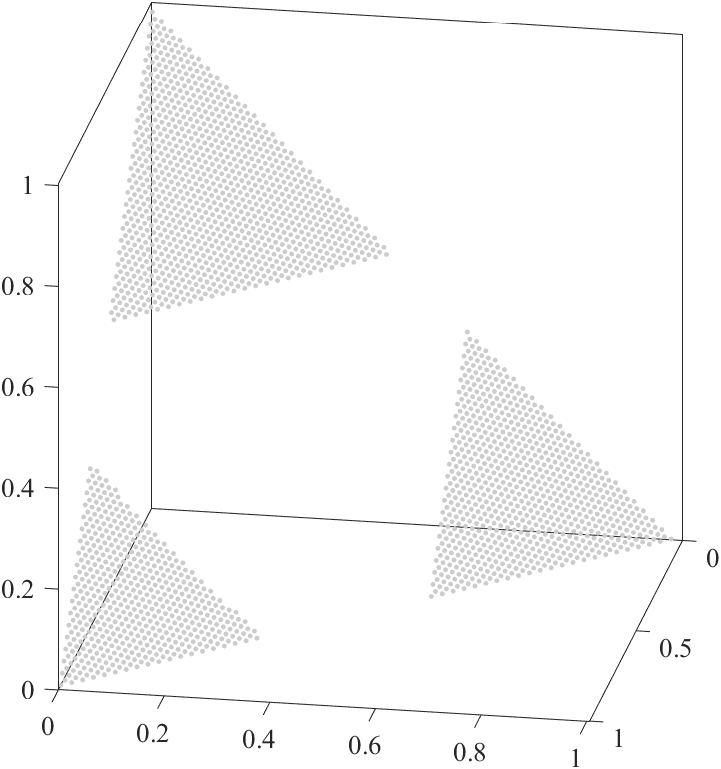
点群Xtestを以下のプログラムで生成します．

A = [0 sqrt(2) sqrt(1/2); 0 0 sqrt(3/2)]'; % 式(15)，(16)の変換行列
alpha = 0.15;                              % アルファシェイプのパラメータ
Xtest = UniformPoint(4960,3,'ILD');
shp = alphaShape(X*A,alpha);
tf = inShape(shp,Xtest*A);
Xtest = Xtest(tf,:);

X*Aのデータから，図3(c)を再現できます．X*Aとshpのデータから，図4(d)を再現できます．
alphaShapeとinShapeは，MATLABの組み込み関数です．リンクから公式情報を確認できます．
点群Xtestとそこから生成した点群Fhat(+点群F)は，以下になります．

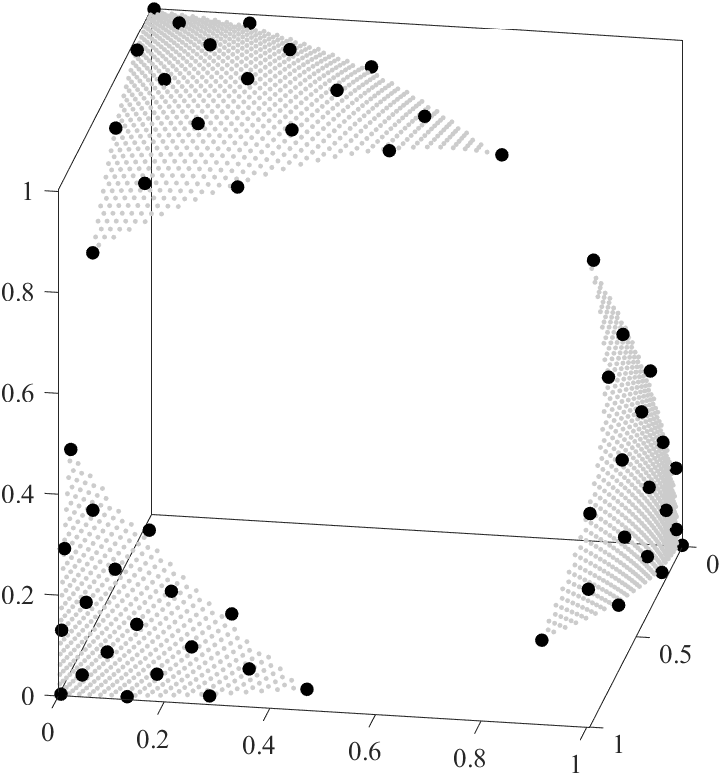
目標となる，図5(d)$\alpha=0.15$を再現することができました．
図の角度と点群Fの黒点を調整すると論文と同一の画像ができますが，わざと少し変更しています．

最後に，今までのまとめとして，点群Fを受け取って点群Fhatを返す短い関数を置いておきます．
PlatEMOユーザーは，こちらの方が分かり易いかもしれません．
いくつかのパラメータはハードコーティングしているので，ご注意ください．

function Fhat = estimatePF(F) % 3次元の点群データのみに対応版
    A = [0 sqrt(2) sqrt(1/2); 0 0 sqrt(3/2)]';
    Y = vecnorm(F,1,2);  % 出力Y：L1ノルム
    X = F./Y;            % 入力X：L1単位ベクトル

    W = UniformPoint(4960,3,'ILD');
    W = W(inShape(alphaShape(X*A,0.15),W*A),:); % validator
    Fhat = W.*sim(newrbe(X',Y'),W')';           % estimator
end

感想・終わりに

情報系では，自身の専門分野の学術誌(Academic journal)に対して，論文掲載を目指す傾向があります．これは，最終的にCellやNature，Scienceへの論文掲載を目指す研究領域と異なります．進化計算学会論文誌への論文投稿を目指す人は少ないと思いますが，少しでも皆さんの参考になれば幸いです．

進化計算学会論文誌に掲載されている論文の多くは，日本語で書かれています．すなわち，日本人のために書かれています．世界で活躍する研究者たちが執筆した日本人を対象とした論文です．無料ですので，是非読んでみてください．

プログラムの参考文献

• Ye Tian, Ran Cheng, Xingyi Zhang, and Yaochu Jin: PlatEMO: A MATLAB Platform for Evolutionary Multi-Objective Optimization [Educational Forum], IEEE Computational Intelligence Magazine, Vol. 12, No. 4, pp. 73-87, 2017.
• Tomoaki Takagi, Keiki Takadama, and Hiroyuki Sato: Incremental Lattice Design of Weight Vector Set, Proc. of Genetic and Evolutionary Computation Conference (GECCO2020), pp. 1486–1494, 2020.