モンテカルロ木探索で一人不完全情報ゲーム「計算」を賢くする[13]

前回、プレイアウト回数を１０００にすることで、そこそこ成功することが確認できた。

それで、まず、プレイアウト回数を変更することで、成功率がどのように変わるか、１００ゲームのシミュレーションをしてみた。 UCB定数=0.5, 閾値5, ゲーム数100としている。

UCB定数=0.5, 閾値5, ゲーム数100としている。

プレイアウト回数　成功数/100
  1000        17
  2000        28
  5000        40
  10000        53
  15000        59
  20000        65
  30000        72
  40000        69
  50000        77
  100000        80
  200000        86

それぞれのプレイアウト回数にて、１００回ゲームしているだけなので、かなり誤差を含むのだが、傾向ははっきり読み取れる。つまり、プレイアウト回数を増やすと、成功率は上がるようだ。プレイアウト回数が１００００以下では着実に成功率が上昇するのだが、２００００を超えるあたりからプレイアウト回数の上昇が成功率の上昇にすこししか効かなくなってくる。そして、プレイアウト回数が３万回を超えたあたりから、効果はとても僅かなものになっている。

プレイアウト回数を１０万回以上にすると、成功率が８０％を超えるようだ。この調子だと、１００万回プレイアウトすると、成功率９０％の可能性もありそうだ。でも、やめておく。プレイアウト回数の上昇は有効なことが分かったが、限界もあるようだ。とりあえず、プレイアウト回数を増やしてテストするのはこのあたりで止めておく。なにしろ、プレイアウト回数を増やすと計算時間がかかってやってられないのである。

前回、モンテカルロ木探索のキモであるUCBの計算式を示した。

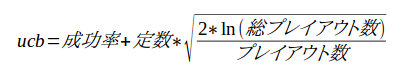
この中に定数があるのだが、いままではとりあえず0.5で試してきた。このUCB定数を変更すると「計算」の成功率がどのように変わるかをじっくり調べてみよう。時間節約のため、プレイアウト回数を10000回で行った。

UCB定数        成功数/100
  0.0        0
  0.0000001    30
  0.000001    21
  0.00001        18
  0.0001        25
  0.001        31
  0.005        32
  0.01        39
  0.05        45
  0.1        54
  0.2        53
  0.5        52
  1.0        53
  10.0        51　

USB定数は、0.1を超えると、ほとんど変化しないようだ。
0.1を切るとどんどん成功率は下がるのだが、0.0001くらいまで下がると、20〜30％程度の成功率に落ち着いて、0.0にすると成功率も一気に０に落ちる。
これから、USB定数は0.1以上だと何でもよさそうに思える。それで、今後は0.5とすることにしよう。 USB定数の値は木の形や成功率（勝率）など、対象が変われば変わると思われるが、追求はこのあたりでお終いにしておこう。

もう１つのパラメータとして、閾値がある。つまり、葉ノード（末端ノード）に対して、最大何回のプレイアウトを行うかによっても成功率が変わるはずだ。

閾値    成功数/100
1    49
2    50
3    51
4    61
5    56
6    63
7    60
8    54
9    55
10    55
20    55

総試行数(ゲーム数)が100回と少ないのであるが、この表から閾値は4〜７あたりが良い感じである。
これは、プレイアウト回数が10000回で行っのだが、プレイアウト回数が増えると、それに伴って最適な閾値も徐々に増加してくるのではと思うが、あまり急激な変化はないようだ。
さて、閾値１というのは、葉のノード１つについてプレイアウト回数が１回ということである。つまり、１００００回プレイアウトしているので、葉ノードが１００００個になっているはずである。これは、木が実をたわわにつけるのではく、枝をどんどん伸ばし、先端の葉にたった１つの実をつけた状態である。そんな状態でも、成功率はたいして落ちないのは興味深い。

今回は、モンテカルロ木探索で調整される一般的なパラメータをいろいろいじって効果を見てみた。
それでわかったことは、とにかくプレイアウト回数を増やすのが良いということだ。
つまり、微妙な調整を頑張るよりも、マシンパワーに頼る方が良い結果が出るというよくある面白くない結果になってしまった。
ということで、次回までに、１００万回プレイアウトという条件で実験しておこう。
そして、次回は、一般的でないことにも挑戦してみようと思う。