ヒント数16のナンプレ問題が発見された

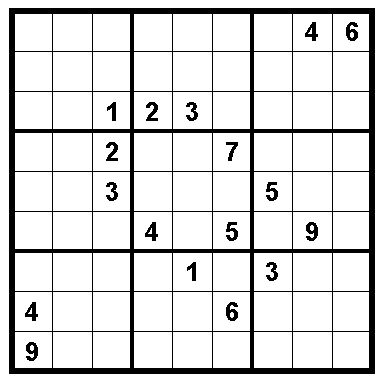
ナンプレの問題は、点対称に数字が配置されていることが多いのだが、ヒント数17では点対称の問題はまだ発見されていないらしい。この問題は、対角線に対して対象にヒントを配置したものであり、難易度はやや高いものの中級程度である。

ヒント数をもっと少なくするにはどうすれば良いだろうか。

ナンプレには、全部で27個の制約条件がある、縦９マスの数字が全て異なるというのが全ての縦列についあるので、これで9個の制約条件がある。横についても同様で、9個の制約条件がある。そして、3×3のブロック内の数字も全て異なるというので、また9個の制約条件があり、全部で27個の制約条件がある。

本当は、一部の制約条件は、他の条件から導かれるのであるが、とりあえず小さいことは無視しよう。

さて、ヒント数を少なくするにはどうすればよいだろうか。

制約条件を増やせば、ヒント数は減らせるはずである。

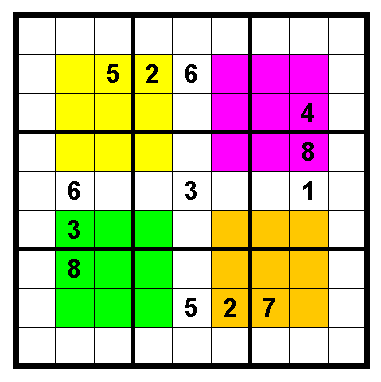
次に示すのは、カラーナンプレ、とくに個の形は Windows　とも呼ばれているようだ。

3×3のカラーの塊があるが、通用のナンプレの制約（ルール）の上に、同じ色の9マスには必ず異なる数字が入るという制約が加わる。そうすることで、この問題の場合、ヒント数を13個まで減らせている。

制約を追加したので、その分ヒントは少なくてもユニーク解となる問題が作れる。

これは自然なことで、アルゴリズム的、あるいは離散数学的には自然な結果である。

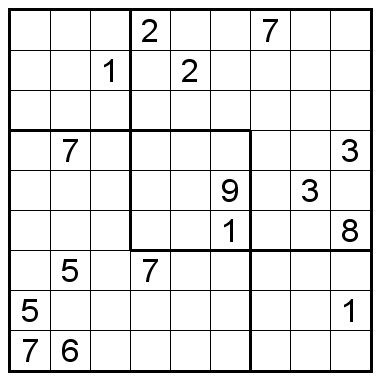
さて、ヒント数16の問題が発見されたということだが、こういう問題である。

よく見ると、3×3のブロックが、対角線上の３つは存在するのだが、それ以外のブロックは区切られていないということで、このL字形の大きな塊の中には、ブロック制約がないということである。

つまり、通常の9×9のナンプレでは、3×3の制約が9個（本当はもっと少なくても、結果的に9個の制約があるのと同じ意味になるが、説明省略）のときには、最少ヒント数が対象性を無視し任意な配置にしても17だったものが、、制約条件を減らすことで最小ヒント数が減るという離散数学的には考え辛い結果がでてきた訳である。

要するに、常識ではそんなことは起きるはずがないという結果が得られたという発表だったのだ。