データ解析のための統計モデリング入門 確率分布と統計モデルの最尤推定 読書メモ

このブログ記事は『データ解析のための統計モデリング入門』（久保拓弥　著、岩波書店）という、とても分かりやすい統計モデリングの入門書を、さらに分かりやすくするために読書メモをまとめたものです。
今回は第２章、確率分布と統計モデルの最尤推定についてまとめます。

この章では主にポアソン分布と、ポアソン分布のパラメータの最尤推定について解説されています。
ポアソン分布とは、下図のような分布です。

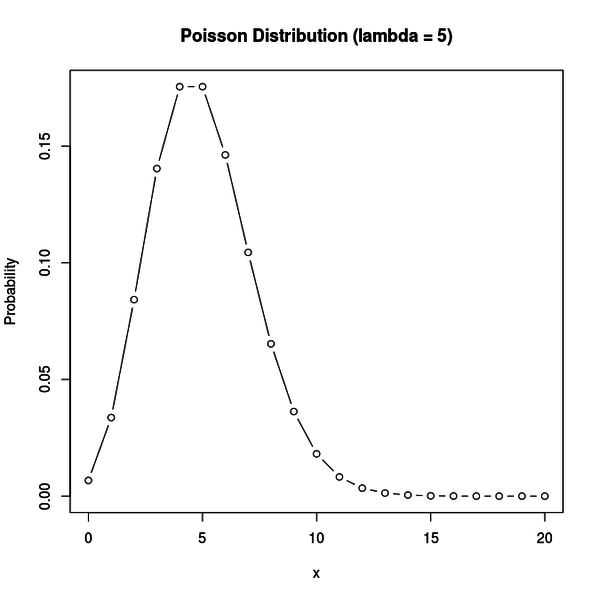
ポアソン分布はパラメータを一つ持っていて、それが決まると分布が決まります。

最尤推定とは、あるデータが得られている時、そのデータが生成される確率が最大になるように、分布のパラメータを選ぶ推定方法です。
データは何でもいいですが、現実の世界で測定された数値です。
その数値をモデルを使って説明しようというのですから、実際に得られているデータに最もよく適合するモデルが欲しいと思うのは当然です。
最もよく適合するというのは、確率の言葉で言えば最大の確率を与えるということなので、このようにパラメータを推定するのが合理的ですね。

さて、問題が単純な場合には、解析的に確率を最大化するパラメータを求めることができるのですが、複雑な問題では普通は数値計算で求めます。
その様子を見やすくするデモを用意しました。
コードはRで書きました。

n <- runif(1, 1, 10)
data <- rpois(20, lambda=n[1])

cat("input data taken from Poisson distribution (lambda = ", n[1], ")\n\n")
data
summary(data)
cat("\n")

cat("likelihood of given data at\n")
res <- vector(length = 10)
for (i in 1:10) {
  prob <- function(x) {
    dpois(x, lambda=i)
  }
  res[i] <- sum(log(prob(data)))
  cat("lambda = ", i, " ", res[i], "\n")
}

cat("\nmaximum likelihood = ", max(res), "when lambda = ", which.max(res), "\n")

このコードが何をやっているか詳しく解説します。
まず最尤推定に使うデータを用意しています。
以下のコードで 1 から 10 までの乱数を一つ用意して、その乱数を平均に持つポアソン分布からサンプルを 20 用意しています。

n <- runif(1, 1, 10)
data <- rpois(20, lambda=n[1])

後は 1 から 10 までの整数 i について、このデータが平均 i を持つポアソン分布から得られる確率を計算しています。
確率を計算しているのは以下のコードです。

prob <- function(x) {
  dpois(x, lambda=i)
}
res[i] <- sum(log(prob(data)))

dpois(x, lambda=i) は λ=i のポアソン分布から x が得られる確率です。
sum(log(prob(data))) は data に含まれる x の全てについて、 dpois(x, lambda=i) を計算し対数を取って和を計算しています。確率の積をそのまま計算すると値が小さくなりすぎて計算できないので対数を取って和を計算しました。ちなみにこの確率には尤度という名前がついています。

後は結果をコンソールに出力しています。
実行結果は次のようになります。

input data taken from Poisson distribution (lambda =  2.923534 )

 [1] 5 3 4 6 5 4 0 2 6 3 6 0 3 4 7 2 1 1 2 2
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
    0.0     2.0     3.0     3.3     5.0     7.0 

likelihood of given data at
lambda =  1   -75.51993 
lambda =  2   -49.77221 
lambda =  3   -43.01152 
lambda =  4   -44.0245 
lambda =  5   -49.29702 
lambda =  6   -57.2638 
lambda =  7   -67.08986 
lambda =  8   -78.27679 
lambda =  9   -90.5031 
lambda =  10   -103.5493 

maximum likelihood =  -43.01152 when lambda =  3

データを生成するのに使われたパラメータは 2.923534 です。
なので、尤度はそれに近い 3 の時に最大になっています。
何度か実行してみると、データを生成するのに使ったポアソン分布の平均に近い時に尤度が一番大きくなっていることが分かると思います。
データの本当の分布は最初に引いた乱数を平均のポアソン分布なのだから、その乱数に近い推定を行った時に、最も当てはまりがよくなるのは順当な結果です。
このように最尤推定を行えば、統計処理したいデータに対し、順当な統計分布を見つけることができるのですね。