この記事では 前回 に引き続き，Microsoft社の製品であるExcelの進化計算を紹介します．
前回は，Excelで進化計算を実行する方法を紹介しました．
今回は，ソルバーのパラメーターについて紹介します．
※変数$\boldsymbol{x}$と目的関数値$f(\boldsymbol{x})$の関係性を表す画像は，MATLABで作成しています．
3つのエンジン
ソルバーのパラメーターには，「解決方法の選択」というタブがあり，3つのエンジンの選択肢があります．
「GRG 非線形」「シンプレックス LP」「エボリューショナリー」の3つです．
エンジンの日本語，英語対応は以下になります．
- GRG 非線形 = Generalized reduced gradient method, nonlinear = 一般化簡約勾配法，非線形
- シンプレックス LP = Simplex method, linear programming = 単体法，線型計画法
- エボリューショナリー = Evolutionary computation, evolutionary algorithm = 進化計算，進化アルゴリズム
問題側から見た場合，説明の記載通りにエンジンを選択することが望ましいです．すなわち，
- 滑らかな非線形性を示す問題 → GRG 非線形 エンジン
- 線形を示す問題 → シンプレックス LP エンジン
- 滑らかではない非線形性を示す問題 → エボリューショナリー エンジン
という選択になります．では，問題と最適化エンジンの組み合わせを変えるとどうなるか見ていきましょう．
滑らかではない非線形性を示す問題
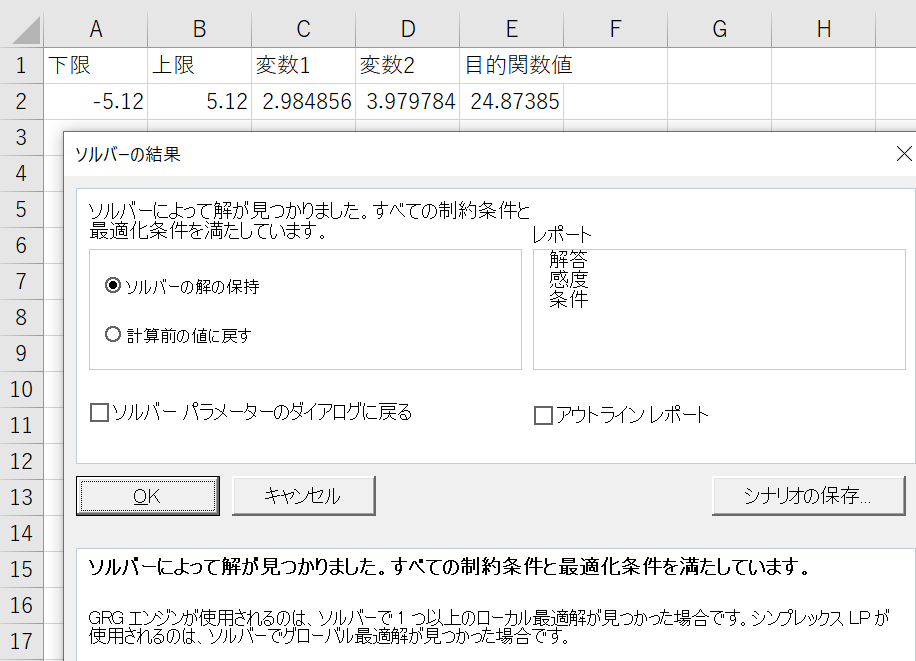
前回実装した Rastrigin function は，滑らかではない非線形性を示す問題になります．
この問題に対して「GRG 非線形 エンジン」を適用した場合，下図のような，役に立たない解を獲得します．
C2セル=「3」，D2セル=「4」の状態でエンジンを実行したため，その近傍の局所最適解が結果になっています．（一応，C2セル=D2セル=「0付近」でエンジンを実行すれば良い解を獲得できます）
この問題に対して「シンプレックス LP エンジン」を適用した場合，下図のエラーが出力されます．
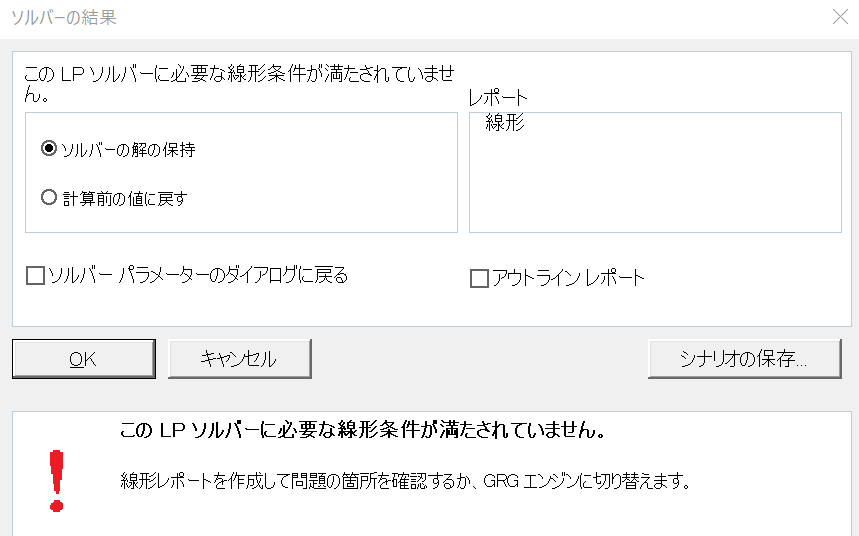
すなわち，滑らかではない非線形性を示す問題は，「エボリューショナリー エンジン」しか対応できません．
滑らかな非線形性を示す問題
問題として，Sphere function を取り上げます．E2のセルを「=C2^2+D2^2」に書き換えます．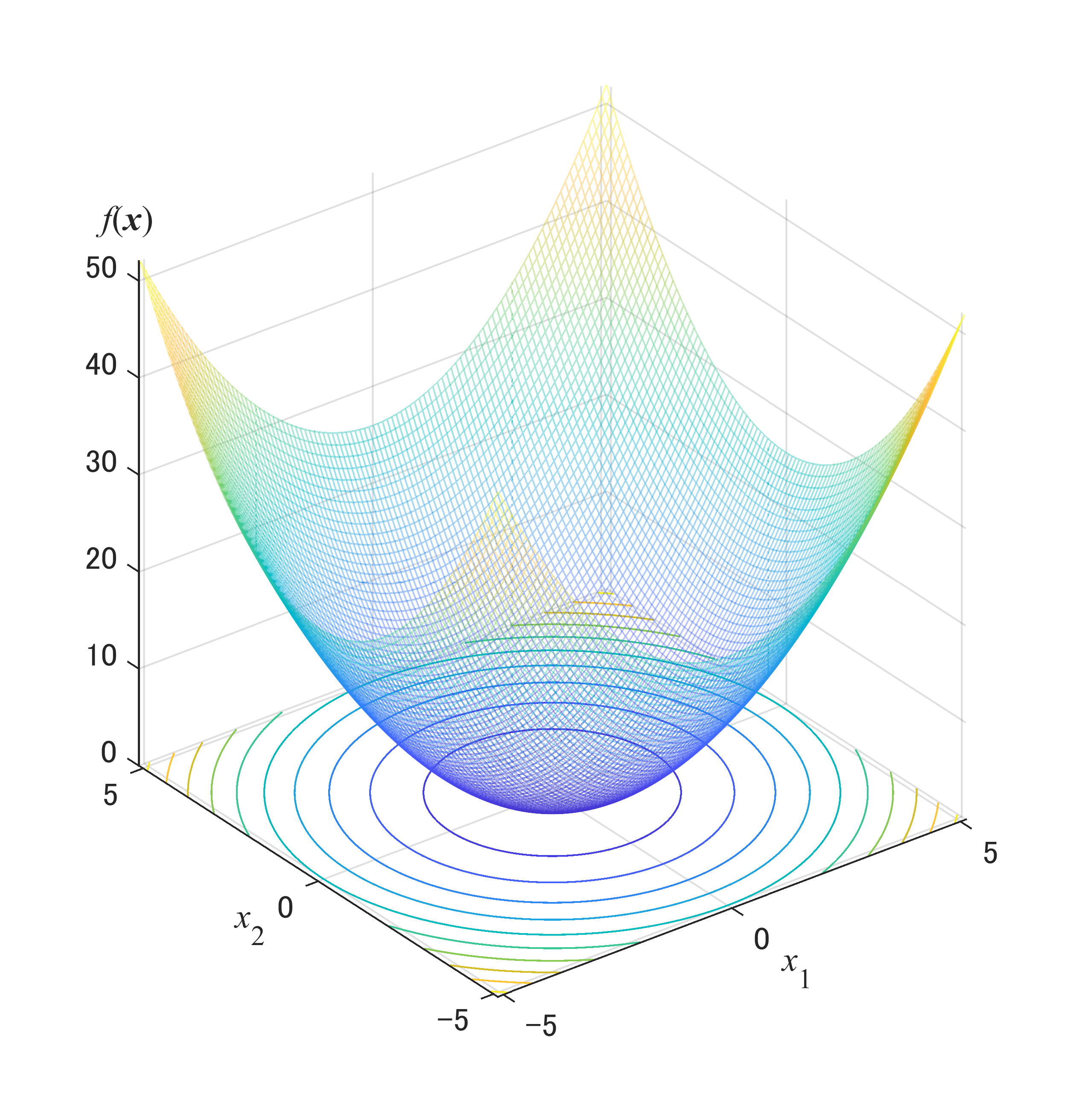
この問題に対して各エンジンを適用した場合，
- GRG 非線形 エンジン → 最適解 (変数1=変数2=目的関数値=0) を瞬時に獲得します
- シンプレックス LP エンジン → エラーが出力されます
- エボリューショナリー エンジン → 下図の結果が得られます
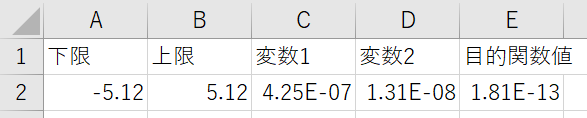
実行時間および精度の面で，「GRG 非線形 エンジン」が適切な選択になります．一方で，90秒程度の実行時間，10万分の1以下の誤差を無視できる場合，「エボリューショナリー エンジン」でも対応可能です．
線形を示す問題
問題として，単純な足し算を取り上げます．E2のセルを「=C2+D2」に書き換えます．
この問題に対して各エンジンを適用した場合，
- GRG 非線形 エンジン → 最適解 (変数1=変数2=-5.12, 目的関数値=-10.24) を瞬時に獲得します
- シンプレックス LP エンジン → 最適解 (変数1=変数2=-5.12, 目的関数値=-10.24) を瞬時に獲得します
- エボリューショナリー エンジン → 最適解 (変数1=変数2=-5.12, 目的関数値=-10.24) を獲得します
精度の面で，3つのエンジンに差は見られませんでした．この問題においても，90秒程度の実行時間と僅かな誤差を無視できる場合，「エボリューショナリー エンジン」で対応可能です．
終わりに
「Excelで進化計算」今回は，Excelソルバーの3つのエンジンと3つの最適化問題を紹介しました．
前回実装した最適化問題は，進化計算エンジンでしか解くことができませんでした．実世界の最適化問題も滑らかでも線形でもない複雑な問題であることが多く，進化計算エンジンしか解けないかもしれません．
進化計算エンジンは，今回紹介した3つの最適化問題を全て解くことができました．最適化問題に出会ったら，「最初に進化計算を実行して，結果を確認する」というのが良い戦略ではないかと思います．
次回も「ソルバーのパラメーター」について紹介します．お楽しみに．
※この記事の「問題を解ける」は，「最適解に近い近似解を獲得できる」ことを意味します．厳密解，精度保証付き近似解が要求されない環境を想定しています．
＃人気の記事
＃タグ
