Excelで進化計算(3)

この記事では，Microsoft社の製品であるExcelの進化計算を紹介します．
前回に引き続き，Excelソルバーのパラメーターについて紹介します．

前回までの復習と今回の内容

前回までに，Excelで進化計算を実行する方法について紹介しました．その中で，

• エボリューショナリー エンジンは，90秒の実行時間が必要だが，紹介した最適化問題を全て解ける
• 紹介した最適化問題を全て解けるのは，エボリューショナリー エンジンのみ

と書きました．これは，実は基本(デフォルト)の設定を採用した場合の話でした．

今回は，オプションから設定を変更することで，以下の2つの課題を解決する方法を紹介します．

• GRG非線形 エンジンは，滑らかでも線形でもない問題を解けない
• エボリューショナリー エンジンは，実行時間が90秒必要

オプションについて

以前に紹介した手順で，ソルバーのパラメーターを開きます．最適化エンジンを選択するタブの右隣にある「オプション(P)」をクリックします．ここから，設定を変更することができます．

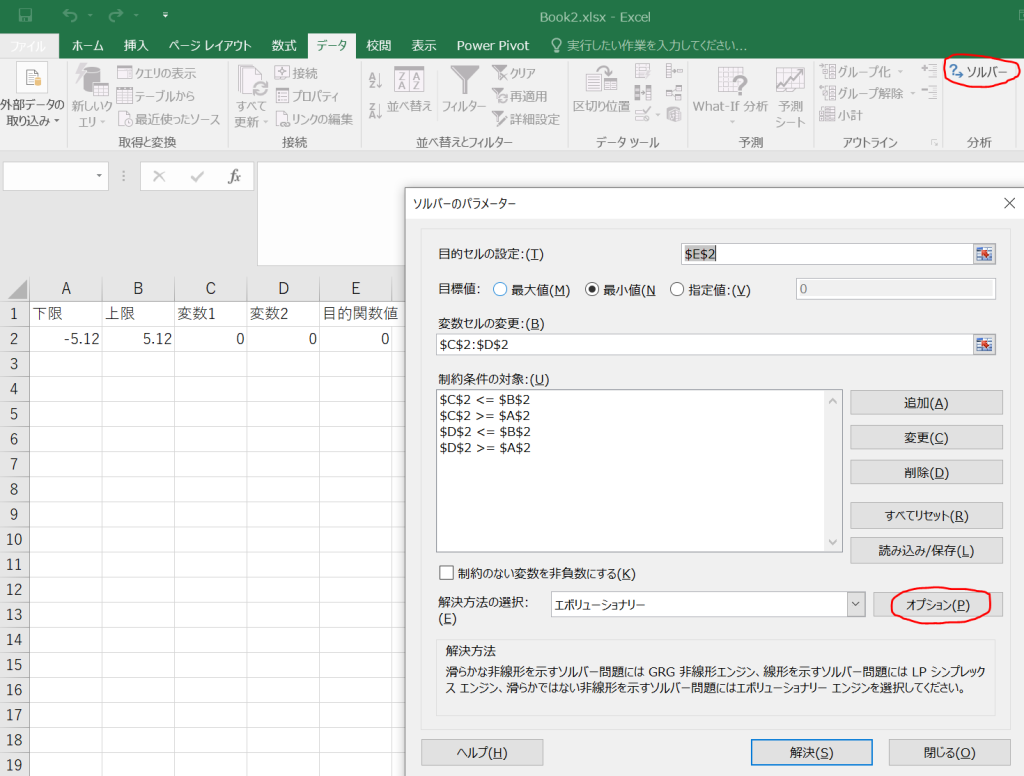
以下が，オプションで変更可能な設定の全てです．

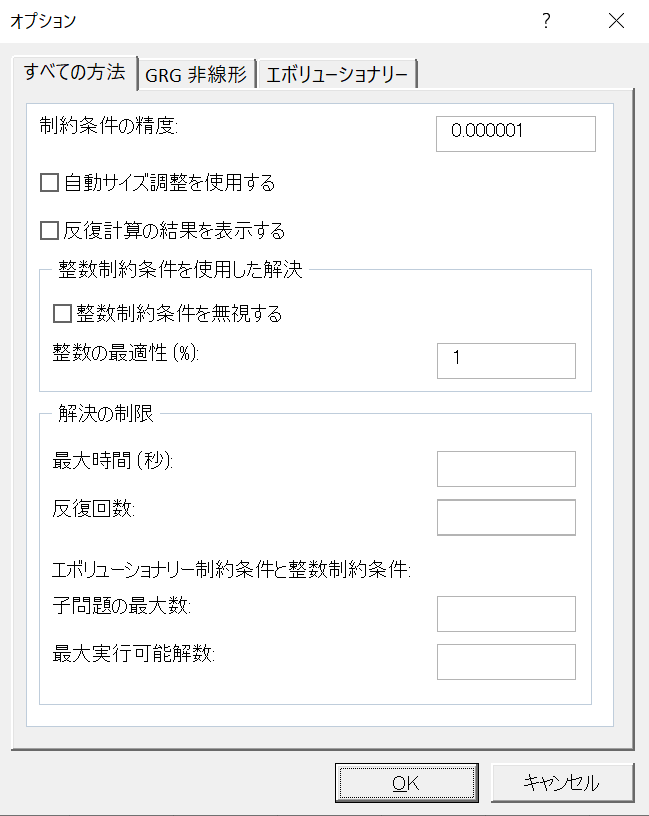
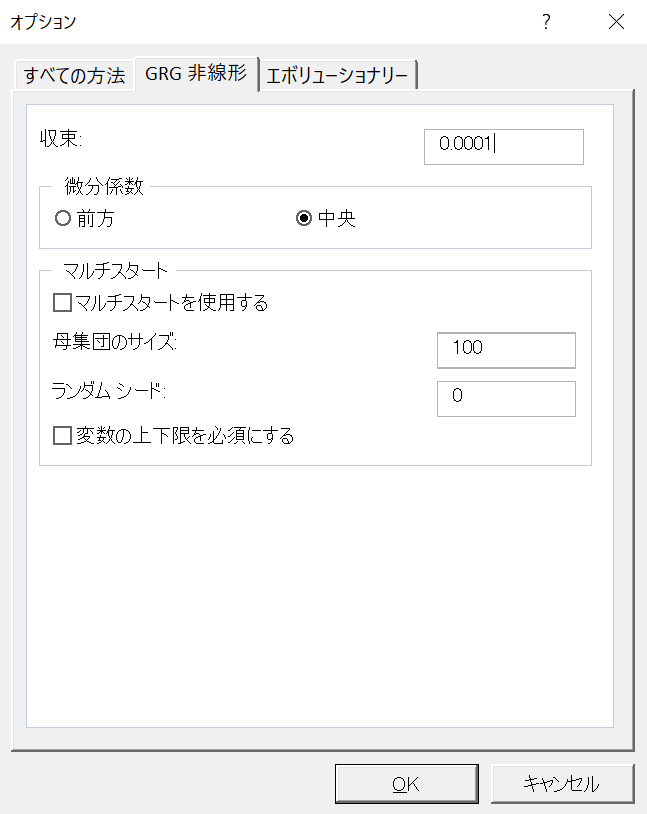
GRG非線形 エンジンで，滑らかでも線形でもない問題を解く

GRG非線形のオプションである「マルチスタートを使用する」にチェックを入れてエンジンを動かすと，滑らかでも線形でもない問題を解くことができます．この方法は，進化計算と同じく，乱数を利用する確率的な手法です．母集団サイズを大きくする or ランダムシードを変えて複数回試行する ことで，より良い解を獲得できる可能性が高まります．

左の図が母集団サイズ100，右の図が母集団サイズ1000で問題（Rastrigin function）を解いた結果です．

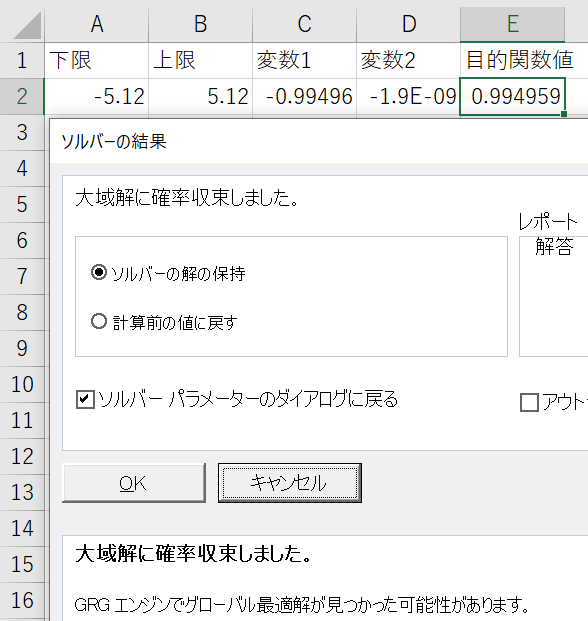
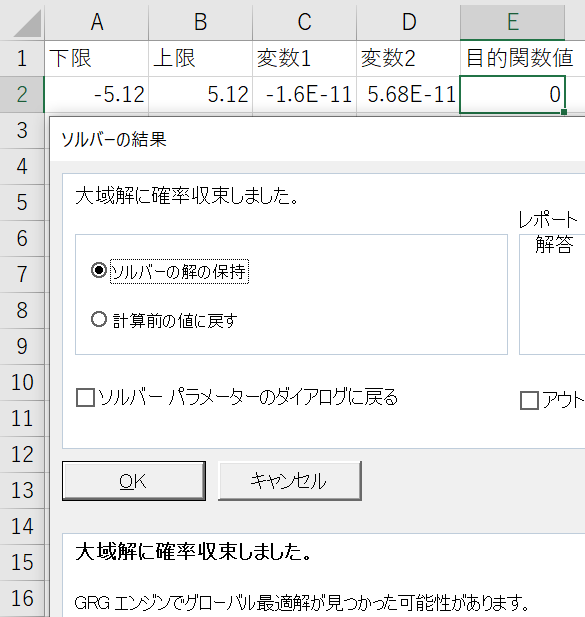
マルチスタート無しの通常のGRG非線形 エンジンは，母集団サイズ1で初期解が入力値で固定されています．母集団サイズ100の場合，通常のエンジンより良い結果ですが，変数値も目的関数値も最適解から離れています．母集団サイズ1000の場合，変数値が最適解に近く，目的関数値0の解を獲得できています．
マルチスタートを使用した場合，通常のエンジンと比較して計算時間は100倍，1000倍に増えますが，それでも5秒もかからずに問題を解くことができます．また，母集団サイズ1000の結果から，Excelの数値計算の精度では，これ以上に最適な解の獲得が難しいことが分かります．（目的関数値で差がつかないため）

「マルチスタート」を使用すれば，GRG非線形 エンジンで滑らかでも線形でもない問題を解けます．

マルチスタート（戦略）とは

マルチスタート（戦略）は，文字通り，複数の解から最適化を開始する戦略です．最適化の最初に，一様乱数やLHSを利用して解を用意します．進化計算やベイズ最適化は，マルチスタートを利用するのが基本です．
マルチスタートのGRG非線形は「ランダムに解を1つ生成して，それを最適化する」ことを繰り返します．すべての計算が独立しているため，他の解の影響を受けません．一方で，進化計算やベイズ最適化は，解同士が相互に影響し合いながら最適化します．交叉や環境選択，確率分布の生成に複数の解の情報を利用します．

以下の画像は，マルチスタートを説明するイメージ図です．（MATLABで作成）

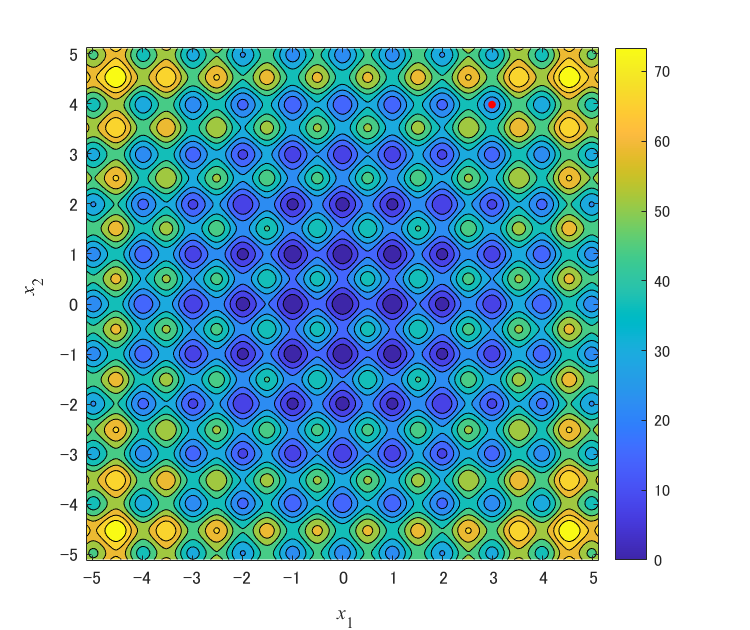
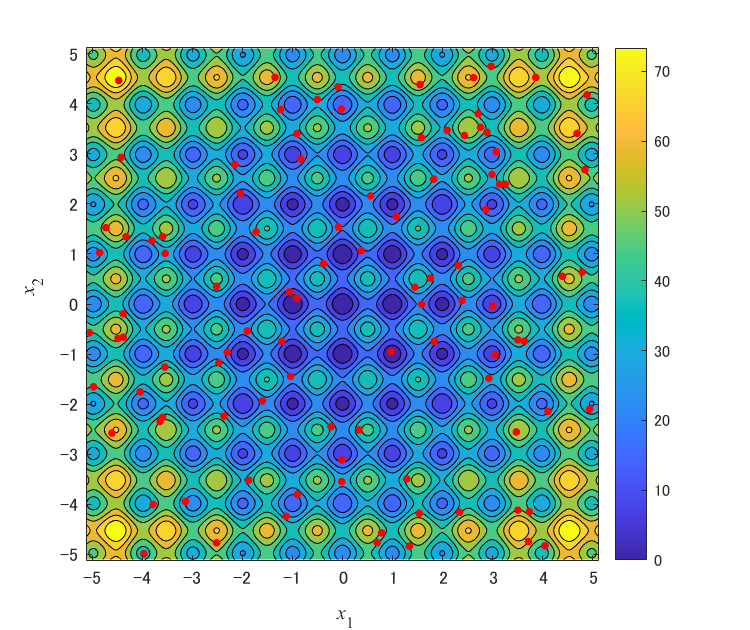
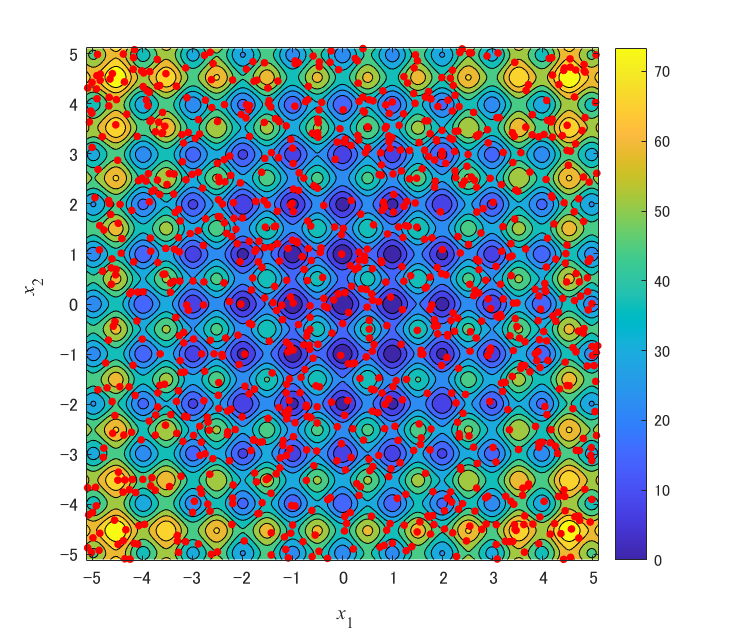
図は，最適化開始時点の様子を表しています．$n=2$次元のRastrigin functionの等高線図を共通してプロットしています．横軸が$x_1$，縦軸が$x_2$，色がその地点の目的関数値$f(\boldsymbol{x})$の値を表します．赤点が解を表します．
マルチスタート無しの通常のGRG非線形 エンジンは，図1のように与えられた1個の初期解から最適化を行い，近傍の局所最適解を獲得します．一方で，マルチスタート有りの場合，図2, 3のように，ランダムに生成した複数の初期解が与えられます．図2は，$(x_1,x_2)=(0,0)$付近に初期解が無いため，$(x_1,x_2)=(-1,0)$付近の局所最適解を最良解として獲得すると考えられます．図3は，$(x_1,x_2)=(0,0)$付近に初期解があるため，最適解に極めて近い解を獲得できると考えられます．

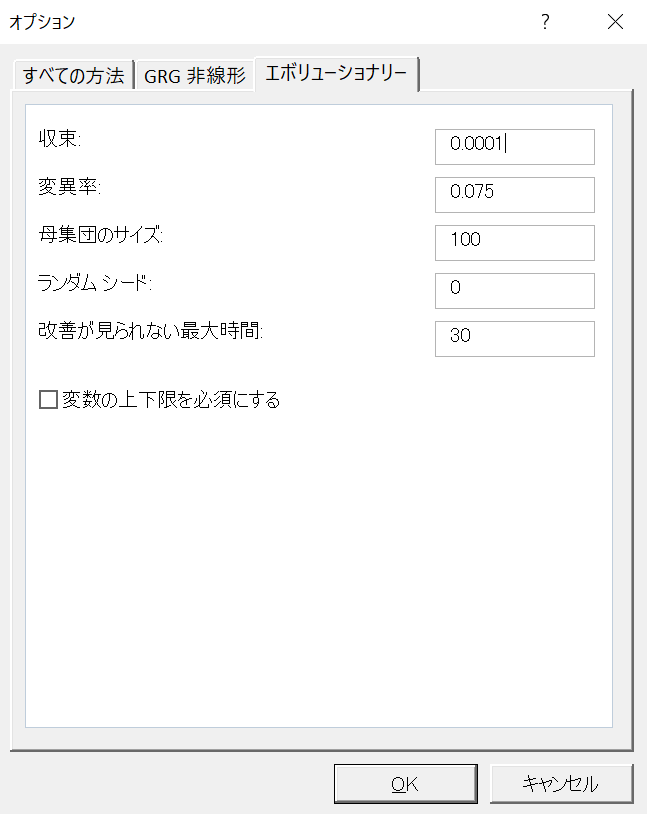
エボリューショナリー エンジンで，短時間で問題を解く

エボリューショナリー エンジンの実行時間が長い一番の原因は，「改善が見られない最大時間」が30(秒)と設定されていることにあります．この値を3などに小さくすることで，劇的にエンジンの実行時間を短くすることができます．他にも，「最大時間（秒）」や「最大実行可能解数」などの「解決の制限」をすることで，エンジンの実行時間を短くすることができます．

プログラムの実行時間を自由に設定できるのは，進化計算の魅力の1つです．他の最適化手法では，実行時間が決まっており，実行時間が短すぎると何も出力できず，実行時間が長くても出来ることが無い場合があります．また，短時間の実行で良い解を獲得できますが，長時間実行できても，より良い解の獲得が困難な場合があります．進化計算は，短時間の実行でも良い解を獲得できますし，長時間実行できるなら，その分より良い解を獲得できる可能性が高いという利点があります．

終わりに

「Excelで進化計算」今回は，オプションから設定を変更することで，課題を解決する方法を紹介しました．
最適化問題を解くにあたっての課題が見つかったとき，別の方法を試す前にオプションの変更を検討してみてはいかがでしょうか．特に進化計算はパラメータやオプションが多く，様々な最適化問題に対して通用する十分なポテンシャルを秘めています．

次回は，「制約条件」について紹介します．お楽しみに．