Excelで進化計算(4)

この記事では，Microsoft社の製品であるExcelの進化計算を紹介します．
今回は，制約条件について紹介します．

制約条件

Excelソルバーのダイアログにおいて，最も大きな面積を占めているのが制約条件に関する表示です．
逆説的に，最適化において最も大切なことは，制約条件の設定と考えることができます．

最初の記事から，変数に上限値，下限値を設定するために4つの制約条件を追加していました．
今回は，この制約条件を変更してみます．

Excelで設定できる制約条件は，全部で6つです．

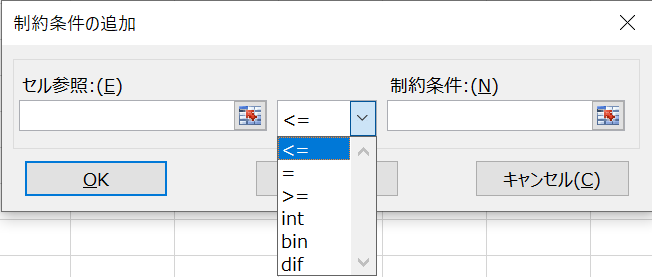
上の3つ<=,=, >=は，左辺と右辺の大小関係を表す比較演算子です．
下の3つint, bin, difは，設定すると=を含む条件に自動で変更されます．
設定すると，intは整数，binは0か1，difは１以上の互いに異なる整数値しか取れなくなります．
difは，セルを範囲指定して使います．右上の設定例では，$A$6:$A$9セルには1,2,3,4や3,1,4,2が入ります．

実行例

=の使用例

総和が100という制限のもと，3変数の総乗を最大化する問題は，以下になります．
　　　　$\text{Maximize }\quad f(\boldsymbol{x}) = \prod_{i=1}^3 x_i = x_1 \times x_2 \times x_3$　　E2セル=A2*B2*C2
　　　　$\text{Subject to}\quad \sum_{i=1}^3 x_i = x_1 + x_2 + x_3 = 100$　　　D2セル=A2+B2+C2

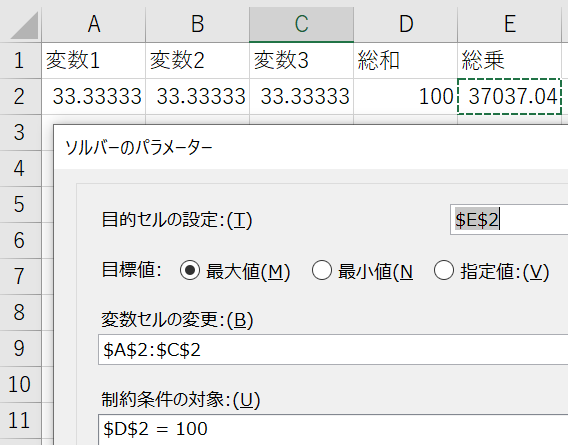
答えは，$x_1=x_2=x_3=100/3$です．

intの使用例

Rastrigin functionの変数を整数に限定します．

　　　　$\text{Minimize }\quad f(\boldsymbol{x}) = 10n + \sum_{i=1}^n [x_i^2 – 10\cos(2\pi x_i)]$
　　　　$\text{Subject to}\quad-5.12\leq x_i \leq 5.12,\quad x_i\in\mathbb{Z},\quad$ for $i = 1,2,\dots,n.$

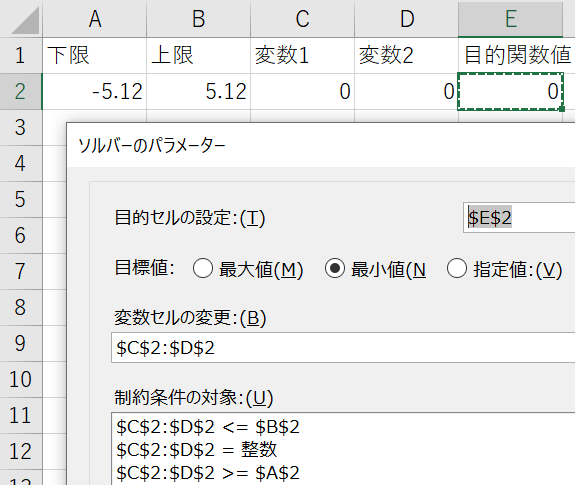
実数値を離散化して整数にすると，最適化問題が解きやすくなる場合があります．

binの使用例

0-1ナップサック問題で考えます．重み$w_i$，価値$v_i$を持つ$n$個のアイテムを取捨選択する問題です．
重量の合計が$W$以下で，価値の合計が最大となる組み合わせを求めます．

　　　　$\text{Maximize }\quad f(\boldsymbol{x}) = \sum_{i=1}^n v_ix_i$
　　　　$\text{Subject to}\quad \sum_{i=1}^n w_ix_i \leq W,\quad x_i\in\{0,1\},\quad$ for $i = 1,2,\dots,n.$

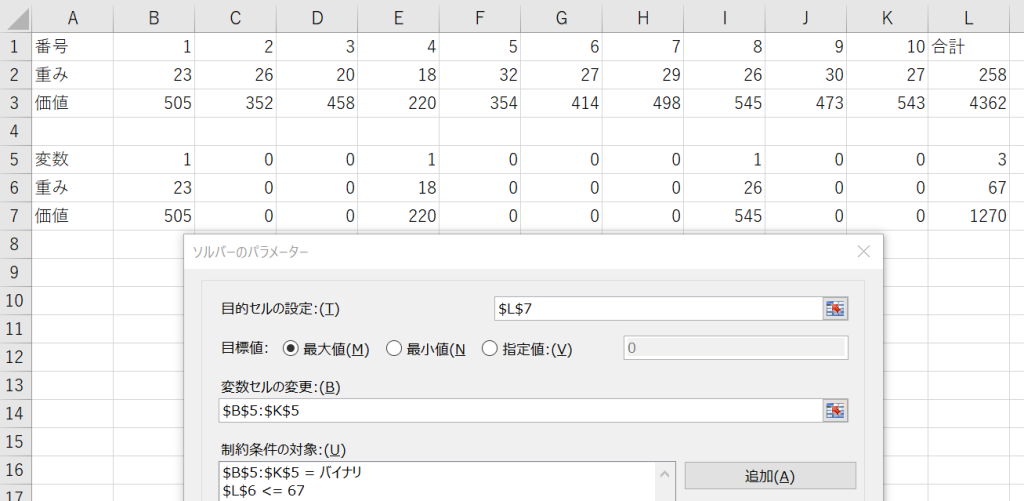
$W=67$の場合，アイテム1, 4, 8を選択する，重量の合計が67で価値の合計が1270の結果が得られました．

difの使用例

$1,2,\dots,n$までの数字をランダムに並べ替えることを考えます．
第$i$要素を$10^i$と掛け合わせた合計の最大化は，以下になります．

　　　　$\text{Maximize }\quad f(\boldsymbol{x}) = \sum_{i=1}^n x_i\times10^i$
　　　　$\text{Subject to}\quad\boldsymbol{x}=\{x\in\mathbb{N^+}|x\leq n\},\quad n(\boldsymbol{x}) = n.$

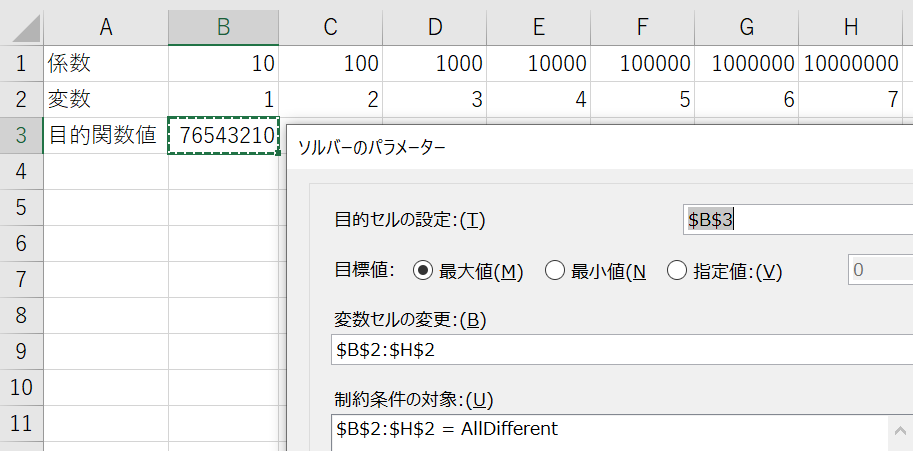
巡回セールスマン問題は，このような順列最適化の代表的な問題になります．

終わりに

全4回の連載記事として，Excelのソルバー機能を紹介しました．記事では，進化計算によって色々な最適化問題を解きました．日常のちょっとした問題をExcelで解決してはいかかでしょうか．