IEEE Access に論文が採択・公開されました

2023年2月28日（火），自身が筆頭著者となる論文がIEEE Accessにて公開されました．
Tomoaki Takagi, Keiki Takadama, and Hiroyuki Sato, “Directional Pareto Front and Its Estimation to Encourage Multi-objective Decision-Making,” IEEE Access, Vol. 11, pp. 20619-20634, 2023.
https://doi.org/10.1109/ACCESS.2023.3250238

この記事では，採択・公開された論文の情報をお伝えします．皆さんの参考になれば幸いです．

基本情報

IEEE Accessは，米国電気電子学会IEEEが2013年に誕生したオープンアクセスの論文誌です．
IEEEが対象とする電気・情報工学の全分野が掲載の対象で，誰でも無料で自由に論文へアクセスできます．
論文掲載時点での掲載料は$1,950(+税，手数料)，評価指標Impact Factorは3.476です．

論文の概要

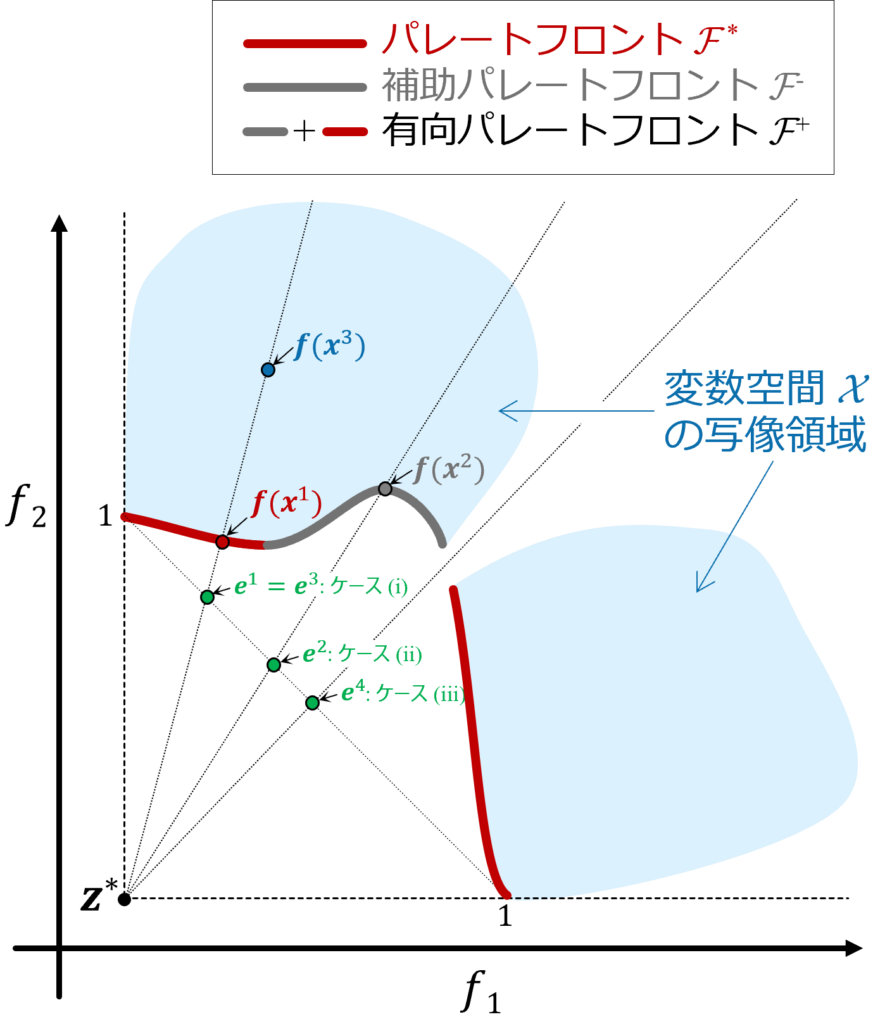
一般的な多目的最適化では，複数の目的間に最適なトレードオフが存在するケースを考え，赤線の獲得を目指します．問題によっては，赤線が複数に分離して存在しますが，その場合でも赤線のみ獲得することを目指します．そのため，赤線の間に解が存在するのか，存在するならどれくらい最適でないのか，疑問に思うことが考えられます．しかし，多目的最適化の考え方では，その疑問に答えることができません．

論文では，複数の目的間の関係性を表す赤線と灰色の線を同時に獲得することを提案しています．灰色の線も獲得することで，図を見た人は，赤線の間にも解が存在することがわかり，赤線の間では目的の値がどのように悪化しているかを知ることができます．また，解の存在する領域が複数に分離しているかがわかります．

進化計算による多目的最適化では，数の限られた解集合（点集合）で最適なトレードオフを表現することを考えます．これをそのまま論文の考え方に適用すると，赤＋灰色の広い領域を解集合で表現しなければならず，その表現粒度は低下します．そこで，解集合から推定した曲線・曲面で最適なトレードオフを表現する方法を提案しています．提案法では，解集合と推定結果を意思決定者に提示できます．

詳細は，論文をご確認ください．

論文の図の再現

ここでは，論文の図3-5の再現方法を紹介します．言語はMATLABです．
図3-5は，DTLZ1S2問題のパレートフロントと有向パレートフロント，それらから推定した応答曲面の図です．
図3は，以下のプログラムで再現できます．

N    = 201;                                        % 曲線を構成する点の数
p    = linspace(0, 1, N);                          % 等間隔に分布するN点の1次元点群
PF   = [p', 1-p']/2;　　　　　　　　　　　　　　　　　% DTLZ1問題のパレートフロント
DPF  = PF .* 2 .* (1 + abs(sin(2*pi*p')) * (2/3)); % 有向パレートフロント，式(3)適用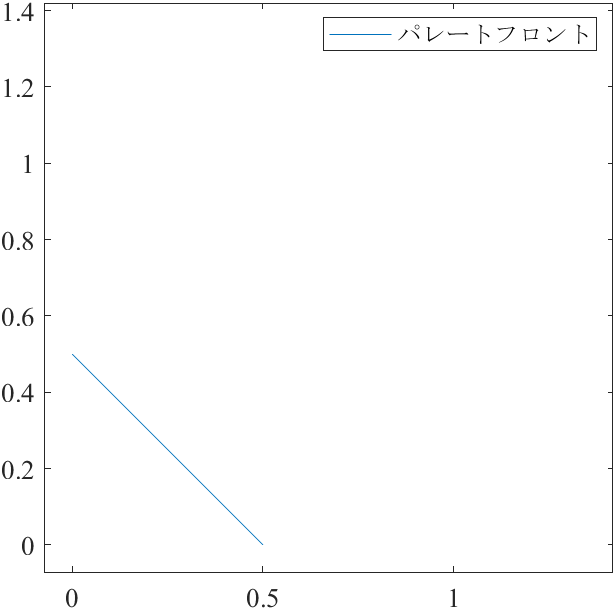

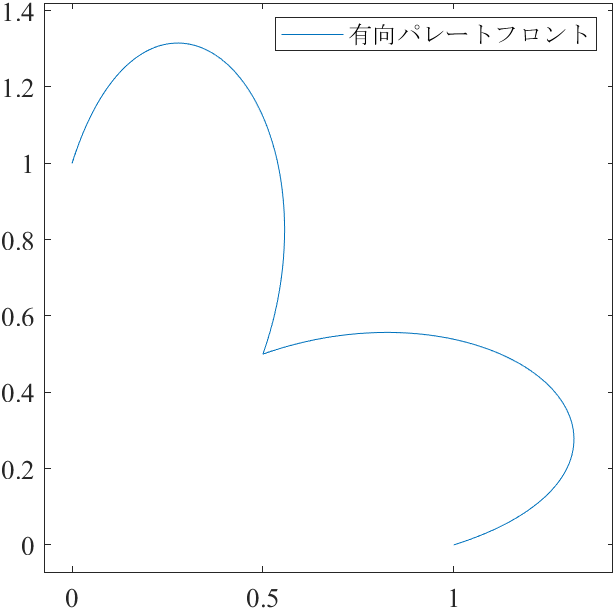
$N=201$個の点群を繋げて曲線を描画します．2目的DTLZ1問題のパレートフロントは，2点$(0.0,0.5), (0.5,0.0)$を結ぶ直線です．論文の式(3)を適用することで，図3を作成できます．

次に，図4(a)と図5(a)は，点群DPFからサブ集合を取り出すことで作成できます．

NDS  = DPF(linspace(1, N, 3), :); % 非支配解集合
DNDS = DPF(linspace(1, N, 9), :); % 非有向支配解集合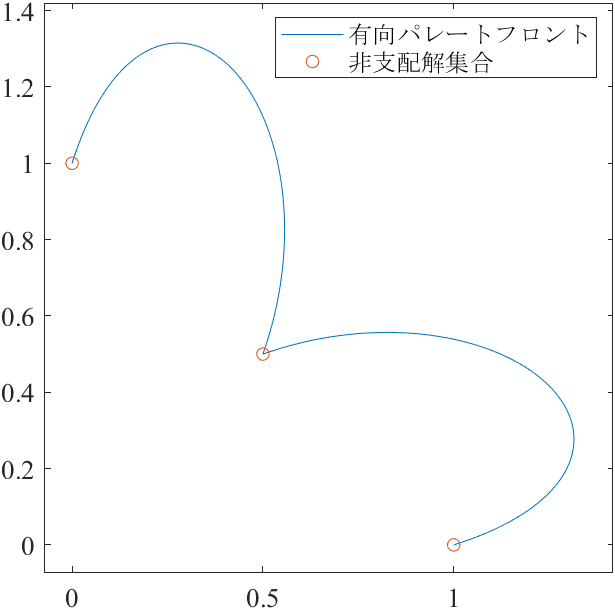

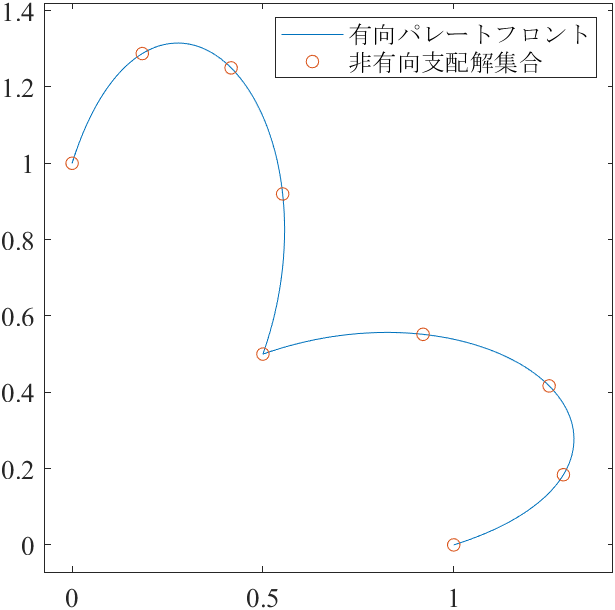
図4(b)と図5(b)の再現には，応答曲面法による推定が必要です．
ここでは，MATLAの組み込み関数fitrgpとpredictを採用して簡易に図を再現します．

y = vecnorm(NDS,　1,　2); % 出力Y：L1ノルム
X = NDS ./ y;         　　% 入力X：L1単位ベクトル
Xtest = [p', 1-p'];　  　 % 推定したいL1単位ベクトル

model = fitrgp(X,y,'BasisFunction','pureQuadratic');
[ypred,~,yint] = predict(model,Xtest);
Pred  = Xtest .* ypred;     % 推定値
Lower = Xtest .* yint(:,1); % 下側の95%の信用区間
Upper = Xtest .* yint(:,2); % 上側の95%の信用区間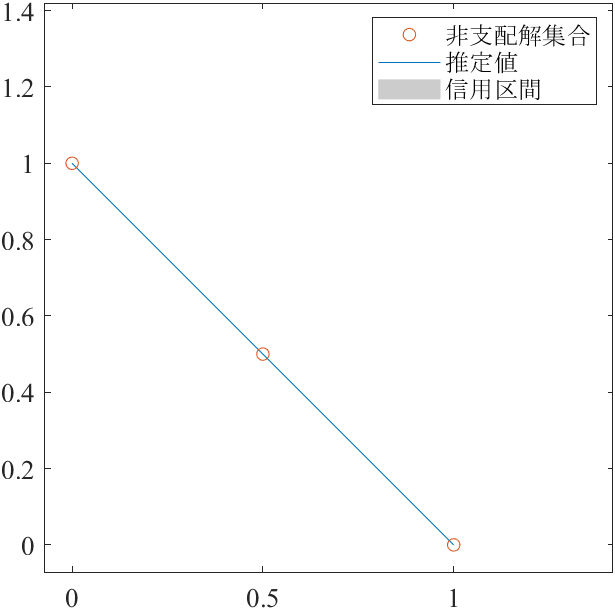

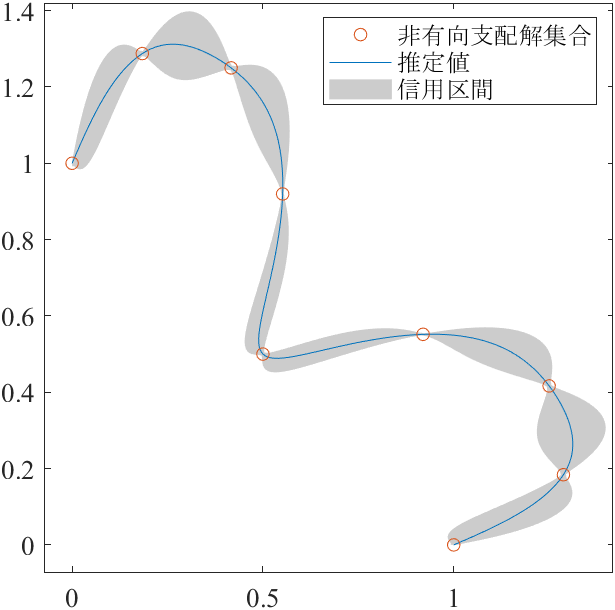
描画を工夫することで，より論文に近い図を作成できます．
オプションが異なるガウス過程回帰やNeural Networkなど，他の応答曲面法で推定すると面白い結果が得られるかもしれません．是非，試してみてください．

終わりに

この記事では，IEEE Accessに採択・公開された論文を紹介しました．
博士で始めた研究を論文誌へ掲載できるように，今後も頑張ります．