Raspberry Pi スパコン (20)　巡回セールスマン問題

MPIを使って、もっと最適化を進めようと思うのだが、まずはじめに、どういう方針でMPIを利用するかを考えよう。

世代数を増やす

前回、100都市、個体数100で、1000世代まで進化させてみたのだが、1回の試行だけで判断するのはよろしくないので、8回実行して重ね合わせてみた。

200世代あたりではかなり差が出ているが、1000世代では最短距離が4234〜4429の間になっていた。
グラフを見る限り、進化はまだ進みそうなので、100都市、個体数100のままで、10000世代まで進化を8回繰り返してみた。

このときの最短距離は3947〜4015になり、より短くなっているし、分散も小さくなっている。

しかし、世代数を10倍にすると時間は10倍かかってしまう。まだ若干進化しつつあるようなので、10万世代まで進化させようとすると、時間が100倍かかってしまう。

個体数を増やす

もう１つは、個体数を増やして実行することである。
個体数を10倍の1000個に増やして、世代数1000のままで実行してみた。

進化の様子は似たようなものであるが、最短距離は3933〜4018になっていて、世代数を10倍するより、個体数を10倍するほうが少し良さそうである。

ただし、個体数を10倍に増やすと、計算時間は10倍では済まなくなる。

MPIによる分散化

以上から、MPIによる分散化(複数のコンピュータへの分散化)について考えてみよう。
個体数を増やすと、最適化の性能は向上するのだが、負荷が増えて、計算時間もかかるようになる。

これを、MPIにより、複数のノードで別々に計算することを考えるのだが、単に分かれていてはだめで、全体としてまとまっていて、１台のコンピュータでは不可能なことが可能になって欲しい。

これを、MPIを使うことで、右のように、複数のノードで進化計算を行うことを考えてみよう。各ノードの個体数が増えなければ、進化にかかる時間は増えないはずである。

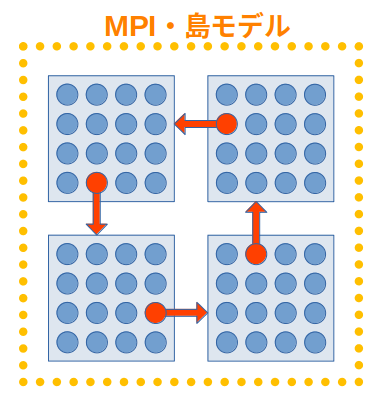
こうすることで、ｎ倍の個体数になったものを、ｎノードに分けて進化計算を行えば、計算時間はほぼ同じで、ｎ倍の個体数のときと同様の最短路が求まらないだろうか。

それぞれのノードを島と考え、島から最良個体を別の島に送ることにしよう。この方法を島モデルと呼ぶ。

ということで、次回から、巡回セールスマン問題のプログラムをMPI対応にして、この仮定が成り立つか確認していこう。