今回から、実際にプログラムの開発を行っていこう。
プログラミング言語はスピードが出る言語でかつそこそこ高機能なら何でも構わないのだが、とりあえずJavaで書くことにした。
今回は、モンテカルロ木探索の有効性を確認するだけなので、ガチガチにコーディング規則に則って書くのはやめて、気楽に書く。動作確認だけなので、GUIは省略し、CUI、それもほとんど出力だけのものにする。
そうなると、プログラムもかなり短くなるはず。Javaなので、当然オブジェクト指向にはなるのだが、いっぱいクラスを作ってということは止めて、一人遊び「計算」のクラス Caliculation を1つだけ用意し、もしクラスにしたいものが発生した場合は、Caliculation内のサブクラスで済ます。
まず、全体で必要な定数を決めておく。
public class Caliculation {
int MAXNUM = 13;
int KUZUNUM = 4;
int DAINUM = 4;
int MAXCOUNT = MAXNUM * DAINUM;大文字にして定数らしさを出しているが、実際に定数にしていないのは、「計算」だけでなく、「コンピュータ」や「超人」さらには、その他のバリエーションにも対応できるようにしたためだ。これらのバリエーションは、コマンド引数で指定することができ、それに従ってこれらの数字を変更してから走らせるためである。
まず、盤面を管理するためのデータを用意する。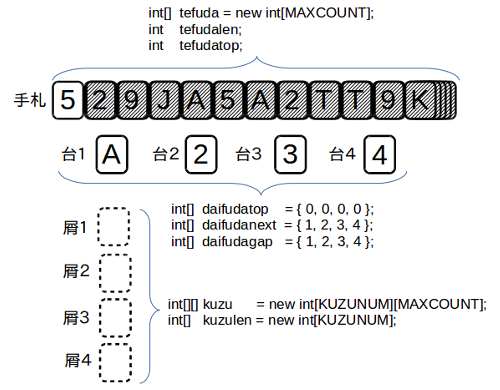 屑札の山はKUZUNUM 個存在し、長さは余裕をもって全カード枚数である MAXCOUNTとしている。
屑札の山はKUZUNUM 個存在し、長さは余裕をもって全カード枚数である MAXCOUNTとしている。
各屑札の山にあるカード枚数も記憶する。
屑札のトップだけが直接参照されるのだが、別に変数を用意することはしない。
手札として、全カード枚数をサイズとする配列 tefuda を用意している。
どんどんカードをめくると手札の枚数が減るが、現在まだ表になっていない手札の枚数をtefudalenとする。
手札のトップは特に重要なので、別の変数 tefudatop を用意する。
手札をめくる行為は、tefudaにある有効なtefudalen枚のカードから1枚を抜いて、tefudatopに移すことである。
台札は、どんどん重ねていくが、トップだけが意味あるので、daifudatopという配列を用意した。
そして、台札はトップ以上に、その上に重ねられる数が重要なので、daifudanextを用意した。
台札に次に重ねられるカードの数字は、台ごとに差が決まっていて、それをdaifudagapに用意した。この値はプログラム実行中に変化することはない。
// 屑札
int[][] kuzu = new int[KUZUNUM][MAXCOUNT];
int[] kuzulen = new int[KUZUNUM];
// 手札
int[] tefuda = new int[MAXCOUNT];
int tefudalen;
int tefudatop;
// 台札
int[] daifudatop = { 0, 0, 0, 0 }; // 台札
int[] daifudanext = { 1, 2, 3, 4 }; // 次における札
int[] daifudagap = { 1, 2, 3, 4 }; // 台札の前の数字とのギャップ(固定)これだけの変数を操作することで、「計算」のカードの動きを全て表せる。
以降の説明では、これらの全カードの状態を「盤面」ということにする。
あと、いくつかの補助的な変数を用意する必要がある。
成功したかどうか、つまり全てのカードが台札に積まれたかどうかの判断が必要なので、まだ積まれていないカードの枚数を示す変数 restcount を用意した。
int restcount = MAXCOUNT;カードの動かし方にはいくつかの種類があり、それを区別するためにenumを使ってみた。
直感的に判りやすいように、4つの動きを漢字で表現してみた。Javaはこういうこともできるということで。
enum MoveType { 手札, 手札台札, 手札屑札, 屑札台札 };
「計算」では、ランダムな操作が頻繁に出てくるので、乱数を生成するためのRandomオブジェクトを1個用意した。
とりあえず、現時刻で初期化している。
Random rnd = new Random(System.currentTimeMillis()); // 乱数このような処理では、乱数は非常に重要で、乱数が乱数になっていないと、良い結果が得られない。
そのため、乱数の使用には最新の注意が必要である。本来なら、メルセンヌ・ツイスタ乱数を使うべきであるが、わかりやすさを優先して(横着をして)標準のもので済ました。
これで、とりあえずデータは揃った。
次に行うべきは、カードの動きを表現することである。 MoveTypeを用意したのだが、それらの4種類の移動タイプがどういうものか、実体を作らないといけない。
移動クラスMove
class Move {
MoveType typ; // 手札、手札台札, 手札屑札, 屑札台札
int fudanum; // 札番号 1〜K
int dainum; // 台札番号 0〜
int kuzunum; // 屑札番号 0〜移動が決まれば、現在の盤面は常にわかっているので、カードの番号は必然的に決まるのだが、とりあえず持っておく。しかし、実際に移動を伴わないタイプが「手札」の場合には、札番号だけが肝心な情報である。
これらを同じ Moveにまとめてしまったので、札番号が入っている。
タイプによっては、不要なデータ項目もあるが、これえらをまとめて、1つのオブジェクトで移動を示すことにした。
Moveオブジェクトの生成は2つ、カードの移動を伴う場合と、手札をめくる場合で別々に用意した。
Move( MoveType tp, int n, int kuzu, int dai ) {
typ = tp;
fudanum = n;
dainum = dai;
kuzunum = kuzu;
}
Move( int n ) {
typ = MoveType.手札;
fudanum = n;
}
次に、この Moveサブクラスの中に、実行メソッドを追加する。
void exec() {
switch( typ ) {
case 手札:
execTefuda(fudanum);
break;
case 手札台札:
execTefudaDaifuda(dainum);
break;
case 手札屑札:
execTefudaKuzufuda(kuzunum);
break;
case 屑札台札:
execKuzufudaDaifuda(kuzunum,dainum);
}
}これでは、タイプ別に異なるメソッドを実行しているだけに過ぎないのだが、判りやすいからこれでよい。
メソッドexecから呼び出される4つのメソッドは、計算全体のクラス、Calculationのメソッドとして用意してある。
全部説明するのは面倒なので、屑札台札の場合だけを説明する。
void execKuzufudaDaifuda( int k, int d ) {
int n =kuzu[k][--kuzulen[k]];
movetodaifuda( n, d );
}屑札の山kから、台札の山dへカードを移す。このメソッドは、必ず移動可能な場合だけ呼ばれるので、エラーチェックはしなくてよい。
まず、指定の屑札の一番上のカードを取り出し、そのカードnを台札の山dへ移すメソッドmovedaifudaを呼び出す。
メソッドmovetodaifudaは、屑札台札の場合だけではなく、手札台札の場合にも共通につかえるので、別メソッドになっている。
void movetodaifuda( int n, int daito ) {
daifudatop[daito] = n;
--restcount;
if( n == MAXNUM ) {
daifudanext[daito] = 0; // 不可能を設定
return;
}
daifudanext[daito] += daifudagap[daito];
if( daifudanext[daito] > MAXNUM )
daifudanext[daito] -= MAXNUM ;
}台札にK(MAXNUM)を移動し終えたら、その台札の山は終了するので、次の台札候補を0にしている。
次の台札の計算を最後にやって終わっている。
こんな感じで、札の移動ができる。
そして、これらを組み合わせると、とりあえずでたらめだけれども、プレイすることだできるようになる。
次回は、今回説明したことを組み合わせて、ルールを守る以外でたらめなプレイをする「プレイアウト」なるものを説明する。



