3D-CGプログラマのための
クォータニオン入門 [増補版]
著者 金谷 一郎
出版社 工学社
定価 2,400円(本体)
頁数 240ページ
判型 A5判
発売 2015年 1月16日
ISBN 978-4-87525-243-6
ちょっと前に読んだ 『ハミルトンと四元数』 がかなり難解だったので、ちょっと易しめの本を読もう、そして3D-CGに関連したものとして本書を選んでみた。
確かにそういう内容で、クォータニオンによる回転などの式変形が丁寧に書かれていた。
しかし、通常、 i, j, k を使って説明される訳だが、本書は違った。
まず、小文字の i,j,k ではなく、大文字のI,J,Kで説明されるが、まあいいかと思っていると、基底ベクトルが次の複素2次正方行列で与えられるのだ。
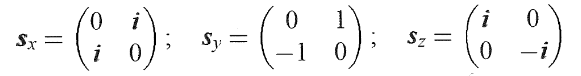 これを元に、3次元の回転が延々と説明される。
これを元に、3次元の回転が延々と説明される。3次元の回転を、複素2次正方行列の演算で延々と説明される。
まあ、ちょっと面食らうのだが、この3つの基底は、i,j,k の場合と同じ性質を持つので、同じ、同値なのだと納得させられる。
つまり、こういうことだ。
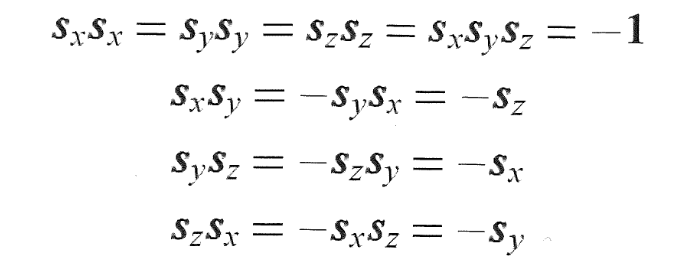 なお、1は、2x2の単位行列と解釈する。
なお、1は、2x2の単位行列と解釈する。そして、なぜか急にパウリが出てきて、物理学の世界に引きずり込まれるのかと思った。
パウリ行列というのは
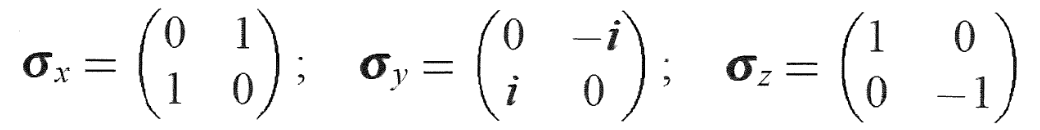 であり、それぞれに 複素数のi を掛けると、最初の sx,sy,sz になるのであった。
であり、それぞれに 複素数のi を掛けると、最初の sx,sy,sz になるのであった。さらに、それが
なんとなく釈然としないところがあるのだが、四元数の追求は一旦終了しようかと思う。



