モンテカルロ木探索で一人不完全情報ゲーム「計算」を賢くする[5]

前回でとても馬鹿なプレイアウトをしたときの成功率を実験する準備ができたので、実行してみた。
10000回やっても、まったく成功しないので、一気に1000000000回、つまり１０億回実行してみた。
その結果、５３３回成功した。

成功率 = 533/1000000000=1/1876173

ということで、とても低い成功率。２００万分の１よりやや良い程度と思われるが、ほとんど成功しないプレイ方法である。


原始モンテカルロ計算

このデタラメにプレイするどうしようもないメソッドを活用して、なんとか賢くプレイするプログラムを作ろうというのが目的であった。
それで、デタラメという言葉で最初に思いつくのが、モンテカルロ法だ。カードを動かすときに、このデタラメプレイアウトを利用して、可能な手の中から一番成功確率の高い手を選ぶというのを毎回行うと賢いプレイにならないだろうか。
図で示すと、次図のようになる。次図の場合、成功率が2/3になった手を選ぶ。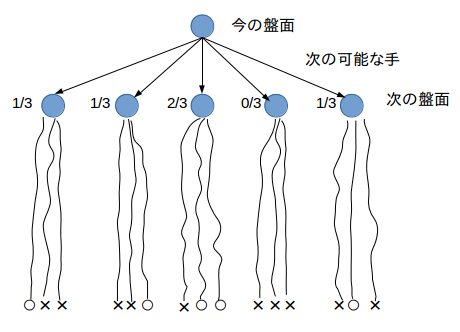

これを実現するために、１回のゲームに対応するメソッドonegameを以下のように書き換えた。

int    onegame() {
        initialize();

        for(;;) {
            opentefuda();

            Move mv = primalMonteCarlo();
            if( mv==null )
                break;
            mv.exec();
        }

        return  restcount;
}

forループの中は、まず手札をめくり、そのあと原始モンテカルロメソッド primalMonteCarloを呼び出している。これを呼べば、実行すべきカードの動きを返してくれるので、それを実行するだけだ。

原始モンテカルロ計算のメソッドが以下である。ほとんどの場合、うまく行かないので、ちょっとだけ工夫してある。

Move	primalMonteCarlo() {
		Move	mv=null;
		
		ArrayList<Move> list = getAllMoves();
		
		int	sz = list.size();
		if( sz==0 )
			return	null;
		if( sz==1 )
			return list.get(0);

		Stock	stock = new Stock();
		double	maxsum = -1.0;
		for( Move m : list ) {
			double	sum = 0.0;
			for( int i=0; i < PLAYOUTCOUNT; ++i ) {
				sum += simpleplayout();
				stock.restore();
			}
			if( sum > maxsum ) {
				maxsum = sum;
				mv = m;
			}
			if( maxsum==0.0 ) {
				PLAYOUTCOUNT = selectRandomly(list);
			}
		}

		return	mv;
	}

最初に、可能なMoveをlistに集め、要素が0個、1個の場合の処理を行う。
２個以上の場合、それぞれのカード移動に対してPLAYOUTCOUNT 回だけプレイアウトを行い、成功率を加算している。なので、実際の成功率は、sum/PLAYOUTCOUNT なのだが、どのカード移動についても同じ回数だけ実行されるので、PLAYOUTCOUNTで割るのは省略した。全てのカード移動に対して、もっとも成功率が高い場合の移動がｍｖに入れたのだが、実はとても問題がある。

プレイアウトsimpleplayoutはとても成功率が低く、1.0になるのは200万分の１程度で、それ以外は0.0となる。そのため、PLAYOUTCOUNTが200万分の１に比べて少ない場合は、maxsumは0.0のままである。このままだと、ほぼ確実に最初の要素がmvになってしまう。

それで、そういう不都合な場合、list中の要素の１つをランダムに選ぶことにした。したがって、プレイが始まって糖分の間は、プレイアウトが無効になって、単にランダムに選ぶのと同じになる。
ということは、このやり方では、成功率はまったく上昇せず、延々と無駄にプレイアウトするので、時間だけ掛かる最悪な状態になる。

次手についてプレイアウトをそれぞれ100回、そしてゲームを100,000回実行してみたが、結果は哀れな状態になった。成功率0、つまり一度も成功することがない。プレイアウト回数、ゲーム回数をもっと増やせば、そのうち０ではなくなるだろうが、測定不能くらい低い成功率である。ということで、これ以上努力するのは止めよう。

さて、どうしようか？

ここで、モンテカルロ木探索の話を持ち出すのが普通だろうが、その前にひと工夫してみよう。
そのまえに、どうして失敗してしまうのか、実際のカードの重なり方の失敗方法を見てみよう。    そのために、現在の盤面の状態をプリントアウトするメソッドを用意した。

Hand: 2 : QQJT56489TAQKAJ3457589TJQKA83456789T
Table: 2(3) 2(4) 6(9) 4(8)
[1] 6J7
[2] 9K
[3] 23
[4] 7K

Handが手札で、トップだけを：の前に書いている。：の後ろは残りの手札を示しているだけである。
Tableは台札を示し、（）内は次における数札を示す。

これを見ると、2や６という絶対台札に出せるカードがあるのに、その上にカードが載せられ、身動きできなくなって自滅の道を進んでいることが分かる。[2]の屑札の一番下に９があるが、Kが上に置かれて使えなくなっている。

この、どうしようもないカードの動きを超簡単なプログラムの変更で何とかできないだろうか？

ArrayList<Move></Move> getAllMoves() {
		ArrayList<Move> list = new ArrayList<Move>();

		for( int k=0; k<KUZUNUM; ++k ) {	// 屑札移動を集める
			for( int d=0; d<DAINUM; ++d ) {
				Move nx = nextKuzufudaDaifuda( k, d );
				if( nx != null )
					list.add(nx);
			}
		}
		
		if( tefudatop == 0 )				// 手札終了チェック
			return	list;
		
		for( int d=0; d<DAINUM; ++d ) {		// 手札台札を集める
			Move nx = nextTefudaDaifuda(d);
			if( nx != null )
				list.add(nx);
		}

		if( list.size() > 0 )			// 台札に載せるのを優先
			return	list;

		for( int k=0; k<KUZUNUM; ++k ) {	// 手札屑札を集める
			Move nx = new Move( MoveType.手札屑札, tefudatop, k, 0 );
			list.add(nx);
		}

		return	list;
	}

まず、これに差し替えて、前と同じように初期状態からプレイアウトしたときの成功率を求めてみる。
同様に１０億回実行すると、494回成功した。
前回５３３回、今回494回の成功なので、何も考えない方が良いという結果が出た。
といっても、この程度の差なので、誤差範囲に入る。
さて、この変更は無意味だったのだろうか。

あまり早く結論を出してはいけない。原始モンテカルロでも試してみた。
前と同じ条件（次の各手に対するプレイアウト１００回、ゲーム回数１００，０００回）で試してみた。
すると、158回成功したので、

成功率　158/100000 = 1/633

何も考えない初手からのプレイアウトの成功率1/1876173と比べると、2964倍成功率が上昇したことになる。一気に上昇したとはいえ、それでも成功率はまだ0.158%に過ぎない。

さて、次はどういう改善をしようか。
そろそろタイトルにしてるモンテカルロ木の話を始めようかな。