 どうやら微分ができることが分かった。
どうやら微分ができることが分かった。といっても、公式として覚えておくべきような簡単なものであった。
今回は、もうちょっと複雑なのをやって、本当に微分できているか確かめよう。
疑い深いのは重要なことである。
難しい式を急に用意しようと思っても、思いつかない。
そういう時は、何かの本のを利用しよう。
と思って背面の本箱を見たら、何とマセマの『微分積分』があった。マセマについては、そのうち紹介しよう。
p77の実践問題9の(2)の微分をしてみよう。
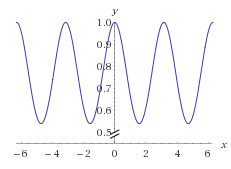
y = cos(sin(x))以下、前回と同じで、式の部分が異なる。
まず、[-π,π] のの区間を20等分してxに入れる。
以下、前回と同じで、式の部分が異なる。
>>> x = Variable(np.array(np.linspace(-np.pi, np.pi, 21), dtype=np.float16)) >>> y = F.cos(F.sin(x)) >>> y.data array([ 1. , 0.95263672, 0.83251953, 0.68994141, 0.58056641, 0.54052734, 0.58056641, 0.68994141, 0.83203125, 0.95263672, 1. , 0.95263672, 0.83203125, 0.68994141, 0.58056641, 0.54052734, 0.58056641, 0.68994141, 0.83251953, 0.95263672, 1. ], dtype=float16) >>> y.grad = np.ones((21),dtype=np.float16) >>> y.backward() >>> x.grad array([ -9.67502594e-04, -2.88574219e-01, -4.48486328e-01, -4.25537109e-01, -2.51464844e-01, 4.06980515e-04, 2.51464844e-01, 4.25537109e-01, 4.48730469e-01, 2.89306641e-01, -0.00000000e+00, -2.89306641e-01, -4.48730469e-01, -4.25537109e-01, -2.51464844e-01, -4.06980515e-04, 2.51464844e-01, 4.25537109e-01, 4.48486328e-01, 2.88574219e-01, 9.67502594e-04], dtype=float16)これで、ちゃんと微分ができているような気がする。
それでは確認だ。
cos(sin(x))の微分を計算してみよう。
・・・ん、どうすれば良いのだろう。 微分を忘れた。
そういう時のために、ネットがある。
例えば、WolframAlphaを使えば、式だけ与えれば、微分だけでなく積分もしてくれる。
WolframAlphaによると、
これを元に、検算をしてみた。
>>> dy = - F.cos(x) * F.sin(F.sin(x)) >>> dy.data array([ -9.67502594e-04, -2.88574219e-01, -4.48486328e-01, -4.25537109e-01, -2.51464844e-01, 4.06980515e-04, 2.51464844e-01, 4.25537109e-01, 4.48730469e-01, 2.89306641e-01, -0.00000000e+00, -2.89306641e-01, -4.48730469e-01, -4.25537109e-01, -2.51464844e-01, -4.06980515e-04, 2.51464844e-01, 4.25537109e-01, 4.48486328e-01, 2.88574219e-01, 9.67502594e-04], dtype=float16) >>> x.grad - dy.data array([ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], dtype=float16) >>> np.max(np.abs(x.grad - dy.data)) 0.0複雑なのでもできるようだ。
この微分で重要なことは、普通のPythonの関数を使うのではなく、chainerで用意されている関数を使わないといけない。そのために、どの関数も F. となっている。
1変数関数をやってきたが、DLは多変数関数というか、超多変数関数を偏微分しないといけないのだ。
次は、そういうことをしようか、でもどうなるかは気分次第。
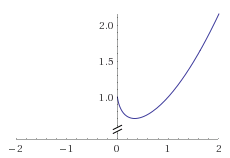
おなじくマセマの微分積分のp79の実践問題10の(1) の微分をしてみよう。
どんなに式が複雑になっても、人間にとって微分が困難になっても、プログラムとしてやることは、ただただ式を記述するだけなので、一気に結果を示す。
>>> x = Variable(np.array(np.linspace(0.1, 2.0, 20), dtype=np.float16)) >>> y = x ** F.arctan(x) >>> y.data array([ 0.79492188, 0.72802734, 0.70410156, 0.70556641, 0.72509766, 0.75878906, 0.80419922, 0.85986328, 0.92578125, 1. , 1.08203125, 1.17285156, 1.27148438, 1.37695312, 1.48925781, 1.60839844, 1.73535156, 1.86816406, 2.0078125 , 2.15429688], dtype=float16) >>> y.grad = np.ones((20),dtype=np.float16) >>> y.backward() >>> x.grad array([-1.01953125, -0.40820312, -0.09423828, 0.11425781, 0.27001953, 0.39892578, 0.50927734, 0.60839844, 0.70019531, 0.78515625, 0.86621094, 0.94433594, 1.01953125, 1.09179688, 1.16210938, 1.22949219, 1.296875 , 1.36230469, 1.42675781, 1.49121094], dtype=float16) >>> >>> dy = x**F.arctan(x) * (F.log(x)/(1+x*x) + F.arctan(x)/x) >>> dy.data array([-1.02050781, -0.40820312, -0.09350586, 0.1137085 , 0.27001953, 0.39868164, 0.50927734, 0.60839844, 0.70019531, 0.78515625, 0.86572266, 0.94384766, 1.01953125, 1.09082031, 1.16210938, 1.22949219, 1.29785156, 1.36328125, 1.42675781, 1.49121094], dtype=float16) >>> >>> x.grad - dy.data array([ 0.00097656, 0. , -0.00073242, 0.00054932, 0. , 0.00024414, 0. , 0. , 0. , 0. , 0.00048828, 0.00048828, 0. , 0.00097656, 0. , 0. , -0.00097656, -0.00097656, 0. , 0. ], dtype=float16) >>> np.max(np.abs(x.grad - dy.data)) 0.00097656さて、次から多変数関数の微分、つまり偏微分をする。



