データ解析のための統計モデリング入門 一般化線形モデル(GLM) 読書メモ３

このブログ記事は『データ解析のための統計モデリング入門』（久保拓弥　著、岩波書店）という、とても分かりやすい統計モデリングの入門書を、さらに分かりやすくするために読書メモをまとめたものです。 今回は第３章、一般化線形モデル(GLM)についてのまとめの三回目です。 この章ではポアソン回帰について説明がされています。 ポアソン回帰によって得られるのは、説明変数と応答変数の分布の関係です。 変数が変化すると別の変数の分布が変化するという、結構複雑な関係が得られるわけです。 分布そのものにも興味はありますが、やはり一番興味があるのは、分布の中でどこが一番確率が高くなるかです。 そこで、本の中で使われているサンプルデータを使ってポアソン回帰をやってみて、得られた分布の中の一番確率が高い場所をプロットしてみました。 コードはRで書きました。

d <- read.csv("data3a.csv")

fit <- glm(y ~ x, data = d, family = poisson)

b1 <- fit$coefficients[1]
b2 <- fit$coefficients[2]

linkFunction <- function(x) {
exp(b1 + b2 * x)
}

fitted <- function(x, y) {
dpois(y, lambda = linkFunction(x))
}

cat("p(y | exp(a + bx)) where p is Poisson distribution\n")
cat("a =", b1, "b =", b2, "\n\n")

y <- 1:20
max <- numeric(length = 20)
for (x in 1:20) {
at <- fitted(x, y)
cat("when x = ", x, ", y = ", which.max(at), " is most probable, probability is ", max(at), "\n")
max[x] <- which.max(at)
}
title <- paste0("p(y|exp(", b1, " + ", b2, "x))")
xl <- "x"
yl <- "the most probable y"
plot(1:20, max, type = "b", main = title, xlab = xl, ylab = yl)

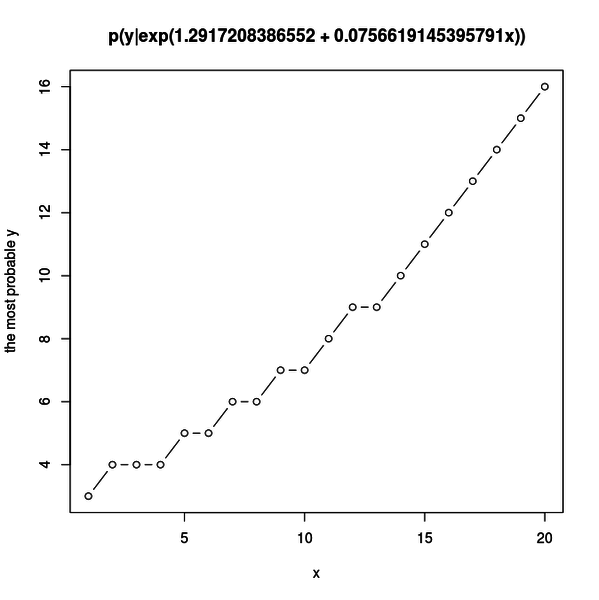
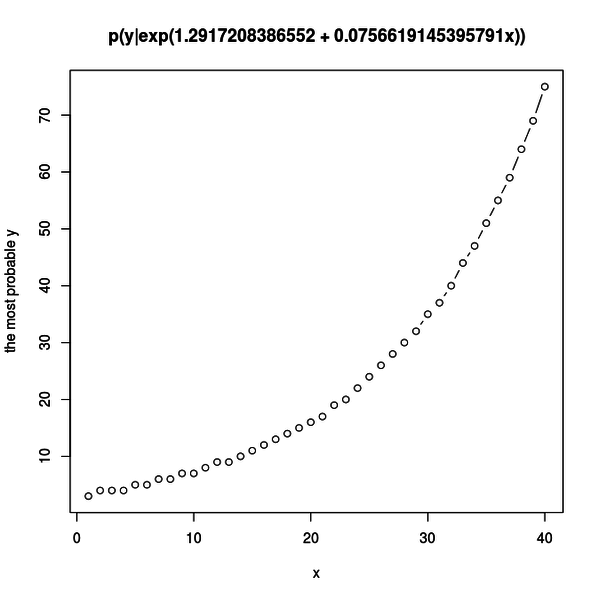
実行すると以下のようなグラフが得られます。 サンプルデータの説明変数 `x` と応答変数 `y` には正の相関があるので、 `x` の増加に従って `y` の分布は大きな値を取るようになります。 グラフを見ると一番高い確率で得られる `y` の値が `x` の増加に従って増えているのが分かります。 正の相関の一面が見られますね。 リンク関数は指数関数なので、もっときれいに指数関数的増加が見られないかとプロットする `x` の範囲を広げてみました。 細かい増加は分かりにくくなりましたが、全体的な指数関数的増加がよく分かるようになりました。