データ解析のための統計モデリング入門 GLMのモデル選択 読書メモ

このブログ記事は『データ解析のための統計モデリング入門』（久保拓弥　著、岩波書店）という、とても分かりやすい統計モデリングの入門書を、さらに分かりやすくするために読書メモをまとめたものです。 今回は第４章、GLMのモデル選択についてまとめます。 この章ではバイアスやAICについて説明がされています。 データを説明するモデルとして様々なモデルが考えられる時に、データへのあてはまりの良さだけを基準にモデルを選ぶことはできません。 それを理解するために、ポアソン回帰で推定されるパラメータがどれくらい真の値からずれるのかを見るためのコードを用意しました。 コードはRで書きました。

legends <- c("ideal", "regression")
ltys <- c("dashed", "solid")
for (i in 1:10) {
y <- rpois(5, lambda = 4)
data <- data.frame(y)

fit <- glm(formula = y ~ 1, family = poisson, data = data)
l <- exp(fit$coefficients[1])

title <- paste("Poisson regression, estimated lambda = ", l)
plot(1:10, dpois(1:10, lambda = 4), ylim = c(0.0, 0.25), type = "l", lty = "dashed", main = title, xlab = "", ylab = "")
lines(1:10, dpois(1:10, lambda = l), type = "l")
legend("topright", legend = legends, lty = ltys)
}

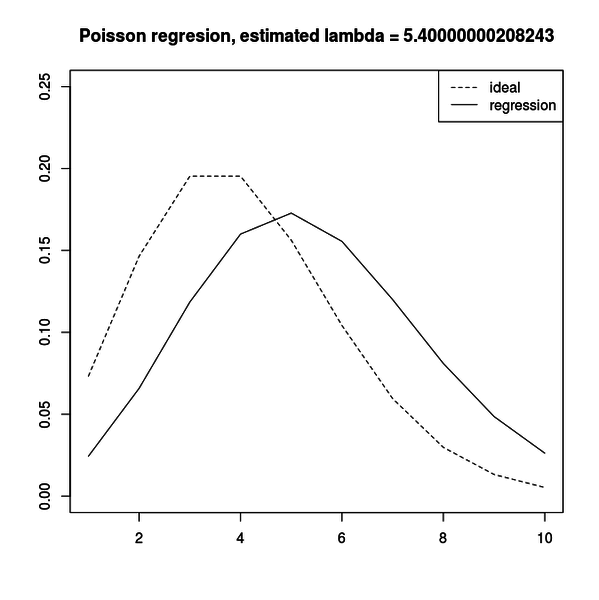
平均 `4` のポアソン分布から5つのサンプルをサンプリングして、そのデータに対してポアソン回帰をしています。 リンク関数は定数です。 正確に推定されるなら、推定されるパラメータは `4` に近い値になるはずです。 実際に実行してみると、5個しかサンプルが無いわりには結構正確に推定されるのが分かります。 しかし、だいたい10回も推定すると、1回くらいは目に見えておかしな推定をするのが分かります。 例えば下図のような推定をします。 真の値は `4` なのに、推定結果は `5.4` です。 このように、与えられたデータに対して最尤推定するしかない以上、推定は推定でしかなくどうしても真の値からずれてしまいます。