データ解析のための統計モデリング入門 GLMの尤度比検定と検定の非対称性 読書メモ6
2017年 04月 04日
このブログ記事は『データ解析のための統計モデリング入門』(久保拓弥 著、岩波書店)という、とても分かりやすい統計モデリングの入門書を、さらに分かりやすくするために読書メモをまとめたものです。
今回は第5章、GLMの尤度比検定と検定の非対称性についてのまとめの六回目です。
この章では尤度比検定などについて説明がされています。
尤度比検定の手法の一つとしてパラメトリックブートストラップ法が説明されています。
対立仮説が正しい場合でも、尤度比検定は必ずしも帰無仮説を棄却できるわけではありません。
そこで、パラメトリックブートストラップ法で帰無仮説を棄却できない場合がどれくらい現れるかを見るためのコードを用意しました。
コードはRで書きました。
createData <- function(n, b1, b2) {
x <- runif(n, 1, 20)
y <- rpois(n, lambda = exp(b1 + b2 * x))
data.frame(x, y)
}
bootstrap <- function(b1) {
simulatedData <- createData(100, b1, 0)
fit1 <- glm(formula = y ~ 1, family = poisson, data = simulatedData)
fit2 <- glm(formula = y ~ x, family = poisson, data = simulatedData)
fit1$deviance - fit2$deviance
}
test <- function(n, b2) {
expData <- createData(n, 0.1, b2)
fit1 <- glm(formula = y ~ 1, family = poisson, data = expData)
fit2 <- glm(formula = y ~ x, family = poisson, data = expData)
dev <- fit1$deviance - fit2$deviance
P <- mean(replicate(100, bootstrap(fit1$coefficient[1]) > dev))
P > 0.05
}
xl <- "Data size"
yl <- "The ratio of failing to reject"
b2 <- c(0.05, 0.07, 0.1, 0.12)
legends <- paste0("b2 = ", b2)
plot(0, 0, type = "n", xlim = c(0, 20), ylim = c(0, 1), xlab = xl, ylab = yl)
n <- 1:20
for(i in 1:4) {
r <- vector(length = 20)
for (n in 1:20) {
r[n] <- mean(replicate(100, test(n, b2[i])))
}
lines(1:20, r, type = "b", pch = i)
}
legend("topright", legend = legends, pch = 1:4)実行するとグラフを1枚プロットします。
最尤推定を 202 * 100 * 20 * 4 回やるので結構時間がかかります。
有意水準としては5%を設定しました。
なので、パラメトリックブートストラップ法を使ってP値を計算し、得られたP値が 0.05 より大きいと帰無仮説を棄却できません。test は検定に使うデータサイズ n と、データをサンプリングする分布の中の説明変数 x の係数 b2 を受け取り、P値を計算して帰無仮説が棄却されなかった場合 true を返します。
あとは、各 n、b2 について、それを100回繰り返して、true が帰ってくる確率を求め、プロットします。
プロットされるのは下図のような図です。
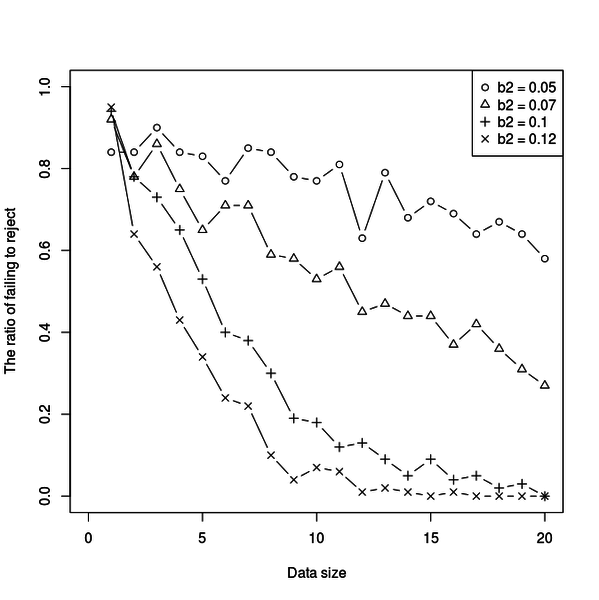
傾向として、データの数が多くなって x との相関が強いほど、帰無仮説は棄却されやすくなるのが分かります。



