データ解析のための統計モデリング入門 GLMの応用範囲をひろげる 読書メモ7
2017年 04月 28日
このブログ記事は『データ解析のための統計モデリング入門』(久保拓弥 著、岩波書店)という、とても分かりやすい統計モデリングの入門書を、さらに分かりやすくするために読書メモをまとめたものです。
今回は第6章、GLMの応用範囲をひろげるについてのまとめの七回目です。
この章では様々なタイプのGLMについて説明がされています。
その中でガンマ回帰について説明がされています。
なので、いろいろなパラメータについてガンマ分布をプロットしてくれるコードを用意しました。
コードはRで書きました。
rs <- seq(0.5, 4.5, by = 1.0)
ys <- seq(0.5, 19.5, by = 1.0)
xl <- "y"
yl <- "Probability"
legends <- paste0("r = ", rs)
for (s in 1:20) {
title <- paste0("Gamma distribution, p(y|shape = ", s, ", rate = r)")
plot(0, 0, type = "n", xlim = c(0, 20), ylim = c(0.0, 1.0), main = title, xlab = xl, ylab = yl)
for (i in 1:5) {
lines(ys, dgamma(ys, s, rs[i]), type = "l")
points(ys, dgamma(ys, s, rs[i]), pch = i)
}
legend("topright", legend = legends, pch = 1:5)
}実行するとグラフが20枚プロットされます。
例えば下図のようなグラフがプロットされます。
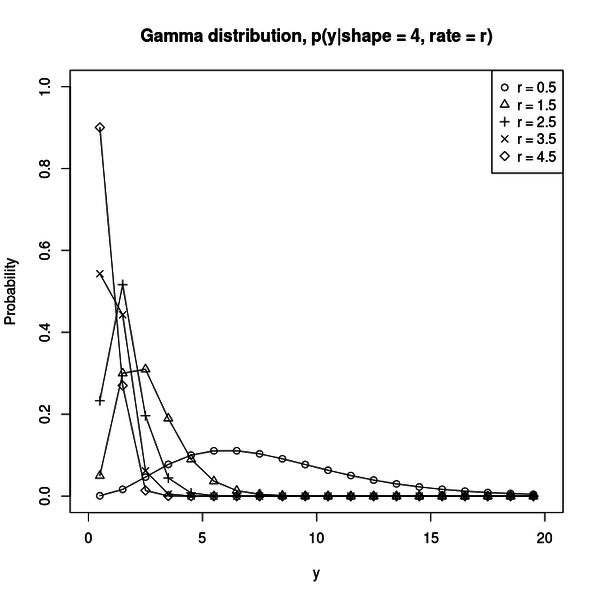
ガンマ分布はパラメータの組によっては、指数分布のような分布や、ポアソン分布のような山なりの分布を取れることが分かります。



