データ解析のための統計モデリング入門 一般化線形混合モデル(GLMM) 読書メモ5

このブログ記事は『データ解析のための統計モデリング入門』（久保拓弥　著、岩波書店）という、とても分かりやすい統計モデリングの入門書を、さらに分かりやすくするために読書メモをまとめたものです。 今回は第７章、一般化線形混合モデル(GLMM)についてのまとめの五回目です。 この章では複数の分布を混ぜて使う、一般化線形混合モデルついて説明がされています。 なので、二項分布と正規分布を掛けた値をグラフにしてくれるコードを用意しました。 コードはRで書きました。

N <- 20

linkFunction <- function(b1, b2, x) {
function(r) {
1 / (1 + exp(-b1 - b2 * x - r))
}
}

distribution <- function(y, linkFunction) {
l <- match.fun(linkFunction)
function(r) {
dbinom(y, N, l(r)) * dnorm(r, mean = 0, sd = 2)
}
}

xl <- "r"
yl <- "Probability"
ys <- seq(0, 20, by = 5)
rs <- seq(-5, 5, by = 0.5)
legends = paste0("y = ", ys)
for (b1 in seq(-0.5, 0.5, by = 0.2)) {
for (b2 in seq(-0.5, 0.5, by = 0.2)) {
for (x in 0:3) {
l <- linkFunction(b1, b2, x)
title <- paste0("logit(q) = ", b1, " + ", b2, " * ", x, " + r, r ~ N(0, 2)")
plot(0, 0, type = "n", xlim = c(-5, 5), ylim = c(0.0, 0.1), main = title, xlab = xl, ylab = yl)
for (i in 1:5) {
d <- distribution(ys[i], l)
lines(rs, d(rs), type = "l")
points(rs, d(rs), pch = ys[i])
}
legend("topright", legend = legends, pch = ys)
}
}
}

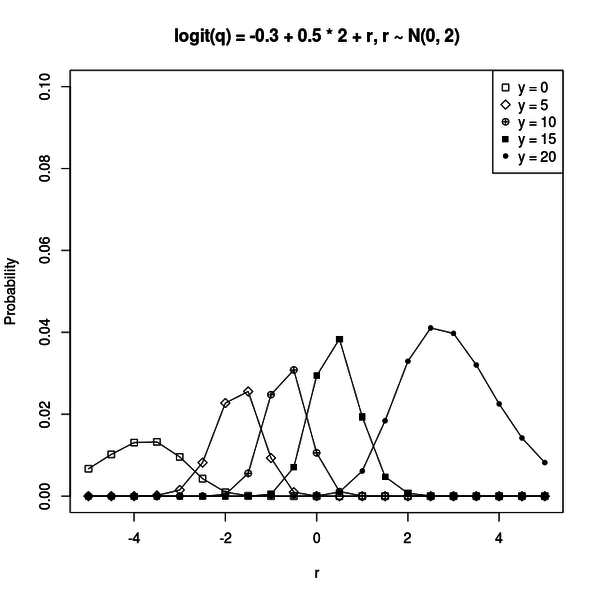
リンク関数は `logit(q) = b1 + b2 * x + r` です。 `r` は平均 `0`、標準偏差 `2` の正規分布から生成される変数です。 事象の試行回数は `20` にしました。 リンク関数を使って二項分布する事象の発生確率 `q` が求まれば、事象が `y` 回起こる確率を計算できます。 あとは、正規分布から `r` が生成される確率と、二項分布を掛け合わせれば、欲しい値になります。 様々な `b1`、`b2`、`x` を与えて、`r` に対して確率をプロットしてみました。 コードを実行すると144枚のグラフがプロットされます。 例えば次のようなグラフが得られます。 `y` によってグラフの山の大きさが変わってくるのが分かります。 混合分布はこれを `r` で積分したものです