データ解析のための統計モデリング入門 一般化線形混合モデル(GLMM) 読書メモ6

このブログ記事は『データ解析のための統計モデリング入門』（久保拓弥　著、岩波書店）という、とても分かりやすい統計モデリングの入門書を、さらに分かりやすくするために読書メモをまとめたものです。 今回は第７章、一般化線形混合モデル(GLMM)についてのまとめの六回目です。 この章では複数の分布を混ぜて使う、一般化線形混合モデルついて説明がされています。 なので、二項分布と正規分布を混ぜ合わせた混合分布をグラフにしてくれるコードを用意しました。 コードはRで書きました。

N <- 20

linkFunction <- function(b1, b2, x) {
function(r) {
1 / (1 + exp(-b1 - b2 * x - r))
}
}

distribution <- function(s, linkFunction) {
l <- match.fun(linkFunction)
function(y) {
sum <- 0
for (r in seq(-100, 100, by = 0.1)) {
sum <- sum + dbinom(y, N, l(r)) * dnorm(r, mean = 0, sd = s) * 0.1
}
sum
}
}

xl <- "y"
yl <- "Probability"
xs <- c(-5,-2,0,2,5)
ys <- 0:20
legends = paste0("x = ", xs)
for (b1 in seq(-0.5, 0.5, by = 0.2)) {
for (b2 in seq(-0.5, 0.5, by = 0.2)) {
for (s in c(0.1, 0.5, 1, 1.5, 2)) {
title <- paste0("logit(q) = ", b1, " + ", b2, " * x + r, r ~ N(0, ", s, ")")
plot(0, 0, type = "n", xlim = c(0, 20), ylim = c(0.0, 0.5), main = title, xlab = xl, ylab = yl)
for (i in 1:5) {
l <- linkFunction(b1, b2, xs[i])
d <- distribution(s, l)
lines(ys, d(ys), type = "l")
points(ys, d(ys), pch = i)
}
legend("topright", legend = legends, pch = 1:5)
}
}
}

リンク関数は `logit(q) = b1 + b2 * x + r` です。 `r` は平均 `0` 、標準偏差 `s` の正規分布から生成されます。 `r` を生成する正規分布の標準偏差が0に近い数の時は、これはロジスティック回帰のリンク関数とほとんど同じです。 混合分布は二項分布と正規分布をかけて `r` で積分したものです。 今は単純に `r` を `-100` から `100` まで `0.1` 刻みで変化させて、面積の合計を求めておきました。 コードで言うと以下の部分です。

for (r in seq(-100, 100, by = 0.1)) {
sum <- sum + dbinom(y, N, l(r)) * dnorm(r, mean = 0, sd = s) * 0.1
}

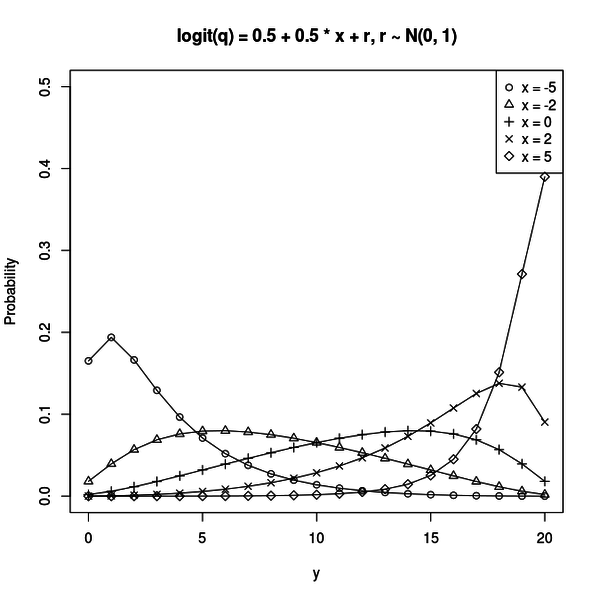
これで様々な `b1`、`b2`、`s` について混合分布のグラフをプロットできます。 コードを実行すると180枚のグラフがプロットされます。 例えば次のようなグラフが得られます。 この図は `b1 = 0.5`、`b2 = 0.5`、`s = 1` の場合です。 二項分布とはたいぶ違った分布が得られているのが分かります。