10月7日、8日2日間連続で行われるMATH POWER 2017 で出題される巨大パズルの準備をしている。
巨大パズルと言うのも色々考えられるが、MATH POWERということで、MATHな問題でなければいけない。
MATHというと、すぐに計算を考えるかもしれないが、いわゆる計算とは違う分野があり、そのようなパズルもある。
ということで、制約充足問題にした。
こういう説明では分かり難いな。
パズルの多くは、制約充足問題なのだ。
ルールという制約があり、問題が与えられ、全ての空欄を、ルール違反せず埋めるのが制約充足問題である。
だから、パズルで、今回は巨大なパズルになった。
で、選択したパズルは、ナンプレである。もとを辿ると、数学者レオンハルト・オイラーが考えたラテン方陣にたどり着くのだが、アメリカの建築家ハワード・ガーンズが考えたもので、1979年にアメリカのデル・マガジン社からNumber Placeという名称で出題された。(詳細は、ウィキペディアを参照のこと)
同じパズルが、とくに日本では多数の名称で呼ばれていて混乱もしているが、ここでは日本国内で最も一般的な「ナンプレ」という呼び方をする。
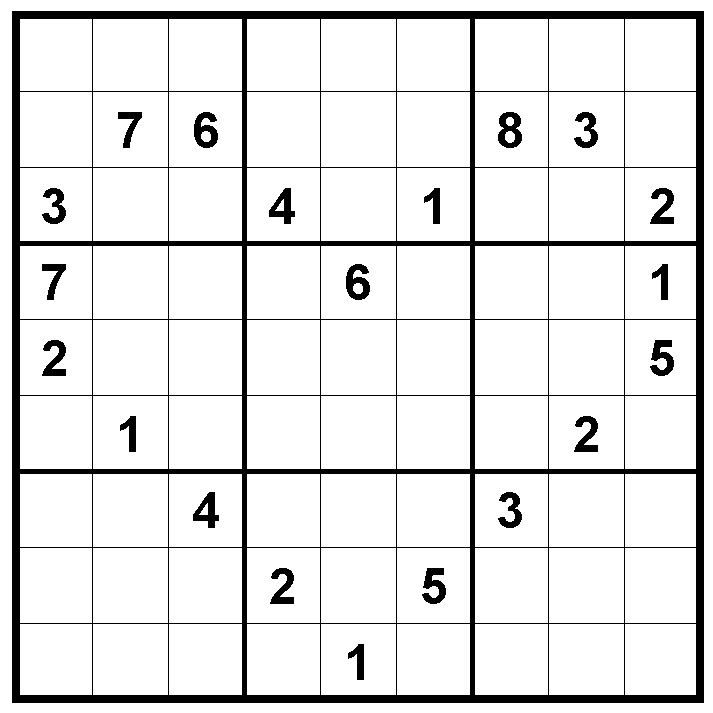
ナンプレのルール
どの縦列にも、1から9の数字が1つ入る。
どの横列にも、1から9の数字が1つ入る。
どの3×3のブロックにも、1から9の数字がはいる。
数字の入っていない空白マス全てに、上記のルールに従って数字を記入せよ。
とても単純な、もろに排他性を利用したパズルである。
とくに計算は何も無い。9種の異なるものなら何でも良い。
「一二三四五六七八九」でもよい。
「鯵鯛鰹鮹鰯鱈鰆鯖鰻」でも構わないのだが、非常にやり難いだろう。
さて、9×9のサイズの問題では、とても巨大とはいえない。
この問題をたくさん出題しても、巨大ではなく、たくさんでしかない。
どうしたら巨大になるだろうか。
9×9ではなく、16x16、25×25、36×36、、、、、81×81、100×100くらいまでいけば巨大かもしれないが、そもそも、そういう問題は作り難い上に、楽しく解いてくれる人がいないのだ。
それで、こんな風にして巨大なパズルにすることにした。
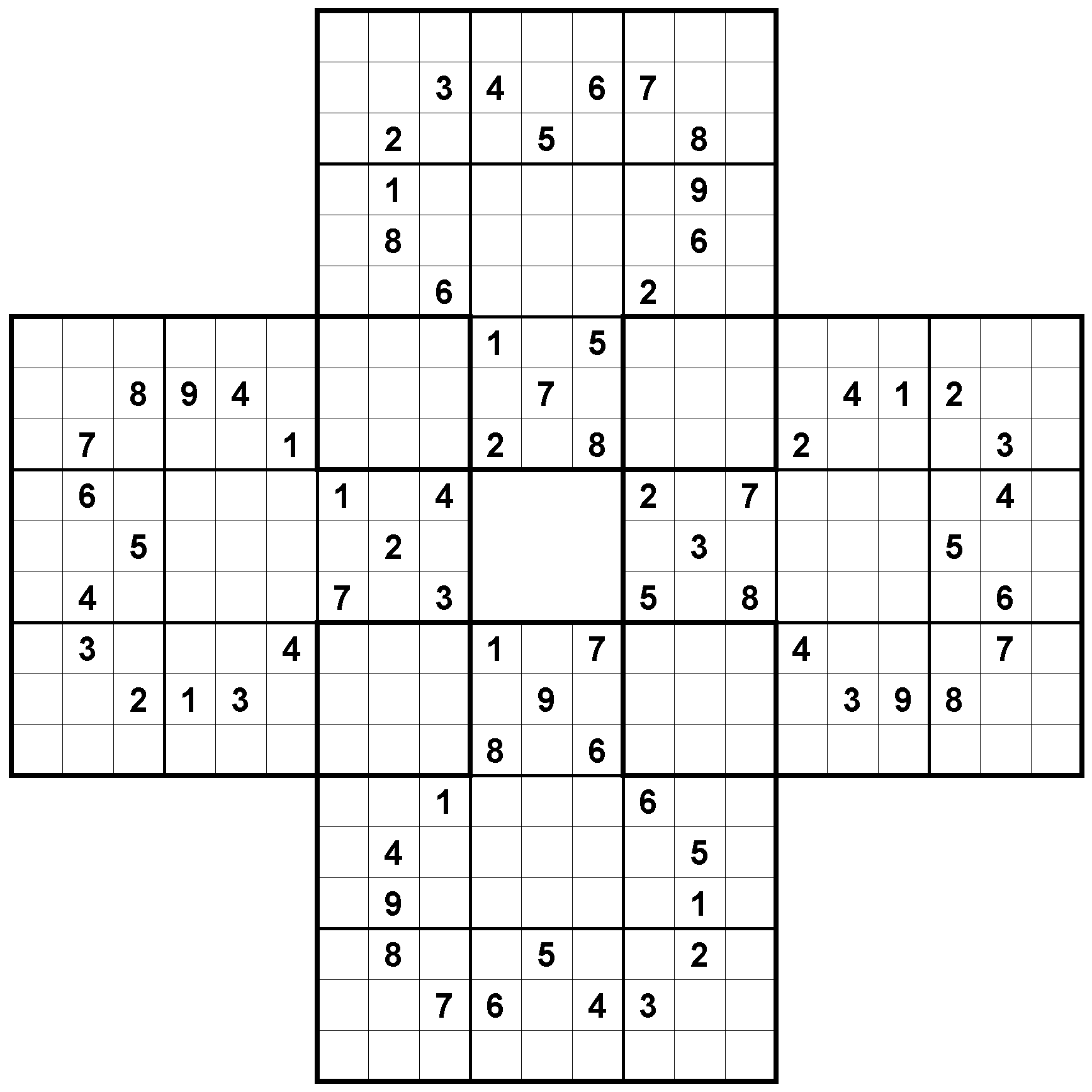
これは9x9の盤面を4枚、ちょうど1ブロックだけ重なるようにして4枚を重ね合わせた例である。 この場合、4枚を合わせたので、4合体という。 重なった部分は、両方に属すると考え、2つのナンプレの制約を同時に満たさなければならない。
上の4合体は、比較的解きやすい問題に仕上げてある。
数字のならびに、発見されやすい細工も入れてみた。
実際に出題される問題は、こんなに小さくはない。もっともっと大きく、作ること自体、現在の技術では限界ではないかというものを提供しようとチャレンジングなことを考えている。
それ以前に、会場で広げられるのだろうか、どうやって印刷すればよいのだろうかなど、様々な困難が待っているようだ。
なにより大変なのは、いままで作ったこともないような合体ナンプレを作ることである。
延々と作らねばならないといっても、毎日延々と徹夜で頑張るのは、人間ではなくコンピュータなのであるが。
巨大パズルと言うのも色々考えられるが、MATH POWERということで、MATHな問題でなければいけない。
MATHというと、すぐに計算を考えるかもしれないが、いわゆる計算とは違う分野があり、そのようなパズルもある。
ということで、制約充足問題にした。
こういう説明では分かり難いな。
パズルの多くは、制約充足問題なのだ。
ルールという制約があり、問題が与えられ、全ての空欄を、ルール違反せず埋めるのが制約充足問題である。
だから、パズルで、今回は巨大なパズルになった。
で、選択したパズルは、ナンプレである。もとを辿ると、数学者レオンハルト・オイラーが考えたラテン方陣にたどり着くのだが、アメリカの建築家ハワード・ガーンズが考えたもので、1979年にアメリカのデル・マガジン社からNumber Placeという名称で出題された。(詳細は、ウィキペディアを参照のこと)
同じパズルが、とくに日本では多数の名称で呼ばれていて混乱もしているが、ここでは日本国内で最も一般的な「ナンプレ」という呼び方をする。

どの縦列にも、1から9の数字が1つ入る。
どの横列にも、1から9の数字が1つ入る。
どの3×3のブロックにも、1から9の数字がはいる。
数字の入っていない空白マス全てに、上記のルールに従って数字を記入せよ。
とても単純な、もろに排他性を利用したパズルである。
とくに計算は何も無い。9種の異なるものなら何でも良い。
「一二三四五六七八九」でもよい。
「鯵鯛鰹鮹鰯鱈鰆鯖鰻」でも構わないのだが、非常にやり難いだろう。
さて、9×9のサイズの問題では、とても巨大とはいえない。
この問題をたくさん出題しても、巨大ではなく、たくさんでしかない。
どうしたら巨大になるだろうか。
9×9ではなく、16x16、25×25、36×36、、、、、81×81、100×100くらいまでいけば巨大かもしれないが、そもそも、そういう問題は作り難い上に、楽しく解いてくれる人がいないのだ。
それで、こんな風にして巨大なパズルにすることにした。

これは9x9の盤面を4枚、ちょうど1ブロックだけ重なるようにして4枚を重ね合わせた例である。 この場合、4枚を合わせたので、4合体という。 重なった部分は、両方に属すると考え、2つのナンプレの制約を同時に満たさなければならない。
上の4合体は、比較的解きやすい問題に仕上げてある。
数字のならびに、発見されやすい細工も入れてみた。
実際に出題される問題は、こんなに小さくはない。もっともっと大きく、作ること自体、現在の技術では限界ではないかというものを提供しようとチャレンジングなことを考えている。
それ以前に、会場で広げられるのだろうか、どうやって印刷すればよいのだろうかなど、様々な困難が待っているようだ。
なにより大変なのは、いままで作ったこともないような合体ナンプレを作ることである。
延々と作らねばならないといっても、毎日延々と徹夜で頑張るのは、人間ではなくコンピュータなのであるが。




