MATH POWER 2017 向けに巨大パズル作成(9) 候補

合体ナンプレを解くとき、マスに入れる数字が１つに決まる場合は良い。
しかし、そういう場合は少なくて、いくつかの数字が入る可能性があるのが普通だ。
マスに入る可能性が残っている数字のことを「候補」という。
何の制約もないとき、マスには１から９までの９個の候補がある（最大）。
しかし、注目しているマスが入っている行、列、ブロックにある数字は、そのマスに入れることができないので、候補から消す。
すると、数個の候補が残る。

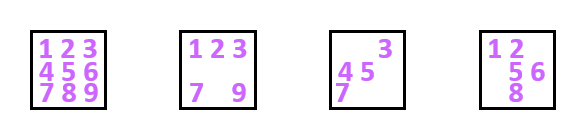しかし、これでも大変だ。

最初に、全ての空きマス（未決定マス）に候補を全部書き込んでいる人を見かける。
９ｘ９のナンプレでも、もし50マス空きがあり、平均４個候補を書こうとすると、200個も数字を書かないといけない。
それに、多数の小さな数字を書き加えると、盤面が非常のごちゃごちゃしてしまう。

そういうこともあって、ナンプレに慣れている人は、少しの候補だけを効率よく書き加えては考えるのが普通だ。
たとえば、こんな感じに書き加える。

ある数字の候補を入れられるマスが9マスよりなる同じ縦列、横列、ブロック内に2マスだけになった場合に書き込むことが多い。
さらに、その2マスが縦か横に2マス連続している場合、2マスの中央（境界線上）に書くことが多い。、

青の丸数字は、初期状態で決まる数字であり、丸の無い青色は、問題およびその後に決まった数字の影響で確定したもの。
そして、小さい紫色の数字が候補である。

上の途中図は、適当な解きかけの状態である。
候補まで考えなくても、まだまだ決められる箇所はあるのだが、全部きちんと調べるのは人間には難しい（コンピュータにはやさしい）。

さて、上の図の状態で、候補同士の影響で決まる箇所がある。

右下のほうを見ると、次のような場所がある。ここで、候補の７に注目してみよう。

右の方の候補７は、横に２つ連続したマスのいずれかに入り、対象となっている横9マスの範囲を矢印で示している。
すると、その矢印の範囲内の左の方に、別の候補７がある。
この候補7は、上下2マスのいずれかを示している。
矢印の線上のマスには７が入らないので、もう一方のマスＡに７が入ることが分かる。

次に、中央よりやや左よりの縦方向で、数字１に注目してみよう。
すると、上の方（Ｂ、Ｃのあたり）に、１の候補が2マスに入るが、縦方向の矢印の縦9マスの一番下に１があるので、この範囲にはもう１は入らない。
ということから、Ｂマスが１に決まり、続いてＣマスが１に決まる。

こんな感じに決まっていく。

こういう横着な候補の書き方を知っていると、247合体も十分に解けるはずだ。

ところで、上の途中図で、６が次々と決まるのだが、その説明は次回にする。