データ解析のための統計モデリング入門 マルコフ連鎖モンテカルロ(MCMC)法とベイズ統計モデル 読書メモ4
2017年 06月 30日
このブログ記事は『データ解析のための統計モデリング入門』(久保拓弥 著、岩波書店)という、とても分かりやすい統計モデリングの入門書を、さらに分かりやすくするために読書メモをまとめたものです。
今回は第8章、マルコフ連鎖モンテカルロ(MCMC)法とベイズ統計モデルについてのまとめの四回目です。
この章ではMCMCやメトロポリス法について説明がされています。
その中で、メトロポリス法によるサンプリングと尤度が関係あることが解説されています。
なので、メトロポリス法によるサンプリングの分布と尤度を比べられるコードを用意しました。
コードはRで書きました。
dataSize <- 20
N <- 8
data <- rbinom(dataSize, N, 0.45)
likelihood <- function (q) {
sum(log(dbinom(data, N, q)))
}
develop <- function(q) {
if (runif(1, 0, 1) < 0.5) {
q + 0.01
} else {
q - 0.01
}
}
sampling <- function(n, init) {
q <- init
ql <- likelihood(q)
samples <- vector(length = n)
i <- 1
while(i <= n) {
p <- develop(q)
pl <- likelihood(p)
r <- log(runif(1, 0, 1))
if (ql < pl || r < pl - ql) {
q <- p
ql <- pl
}
samples[i] <- p
i <- i + 1
}
samples
}
qs <- seq(0, 1, by = 0.01)
ls <- vector(length = length(qs))
for(i in 1:length(qs)) {
ls[i] <- prod(dbinom(data, N, qs[i]))
}
plot(qs, ls, type = "l", xlab = "q", ylab = "Likelihood")
samples <- sampling(10000, 0.3)
hist(samples, breaks = seq(0, 1, by = 0.01), main = "10000 samples", xlab = "q")サンプルデータとしては、本の中でやっているのと同じように、事象の発生確率が 0.45 で、事象の試行回数は 8 の二項分布から、20 個のサンプルを取って用意しました。
コードを実行すると次のような図がプロットされます。
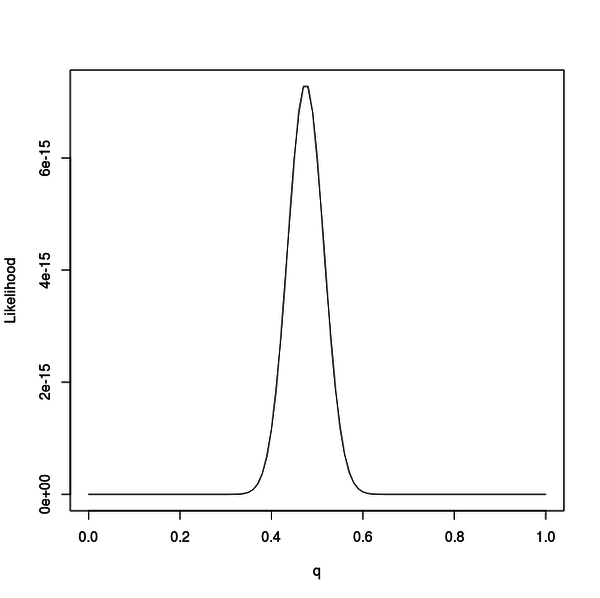
この図は q を変化させた時の尤度のグラフです。
発生させたサンプルデータの偏り方によって多少ずれますが、だいたい 0.45 を中心とした山なりなグラフになります。
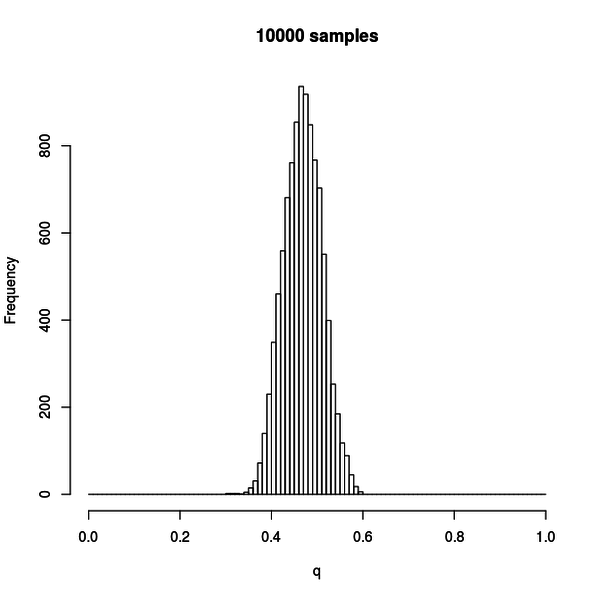
この図はサンプル数 10000 の場合のメトロポリス法によるサンプリングの結果のヒストグラムです。
確かに、さきほどプロットした尤度に比例した分布が得られていることが分かります。



