Octave：逆行列の計算量のオーダーをグラフ化

偏微分方程式の数値解を求めるのに大きなサイズの逆行列を計算する必要があった。
これに限らず、色々な計算をやっていると、逆行列を求める必要にせまられる。それも、かなり大きなサイズで。

ということで、今回は、サイズn の正方行列の逆行列の計算量が、サイズnに対してどのように増えていくかを調べてみる。
要するに、逆行列の計算量のオーダーを求めようということだ。

まず、元のサイズnの正方行列を用意しなくてはならない。それも、逆行列が作れる行列、つまり正則行列を用意しなければならない。

ということで、

A = rand(n);

を考えた。要するに、n*nの正方行列に、0から1の範囲の一様乱数を散りばめただけの正方行列である。

しかし、不安もあるので、これで大丈夫か実験してみよう。

まず、乱数行列を作って、１つの行の半分の値を他の行に書き込むことで正則でなくしてから逆行列を作ってみた。

>> A = rand(4);
>> A(4,:)　=　A(1,:)/2
A =

  0.66039   0.64815   0.31595   0.95572
  0.45772   0.80134   0.98210   0.55091
  0.15502   0.47775   0.87121   0.86565
  0.33020   0.32407   0.15798   0.47786

>> B = A^-1
warning: inverse: matrix singular to machine precision, rcond = 0
B =

  Inf   Inf   Inf   Inf
  Inf   Inf   Inf   Inf
  Inf   Inf   Inf   Inf
  Inf   Inf   Inf   Inf

>>

これで、叱られ方が分かった。



次に、サイズ1000の乱数配列の逆行列を10000回作って大丈夫かどうか確かめた。

>> for i = range(10000)
A = rand(1000);
B = A^-1;
endfor
>>

何も小言は言われなかったので、いい加減にやって大丈夫のようだ。

次に、行列のサイズを100から100ずつ増やして計算時間を tic(), toc() を使って計測し、グラフ化してみた。

k = 1
for n = 100:100:5500
    A = rand(n);
    tic()
    A = A**(-1);
    sz(k) = n;
    tm(k) = toc()/r;
    k += 1;
endfor
plot(sz,tm)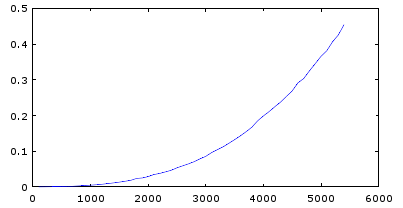

サイズの増大とともに急激に時間が掛かっているのは分かるのだが、指数関数的なのか、ｎの何乗かのオーダーなのかよく分からない。サイズが5400で止まっているのは、メモリ不足でOctaveに叱られたためである。

ということで、まず、指数関数的になっているのか調べるために、片対数のグラフを描いてみた。

semilogy(sz,tm)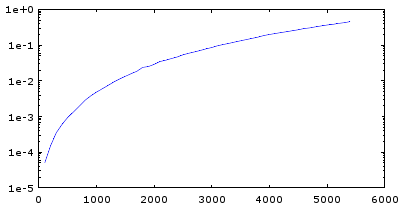

指数関数的には増えていない。もっと緩やかな上昇をしていることが分かる。

最初のグラフから、たぶんn^3程度の割合で計算量が増えていそうなので、計算時間の3乗根(1/3乗)を縦軸にとったグラフを描いてみた。

plot(sz,tm.^(1/3))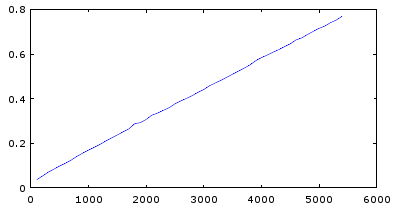

ということで、逆行列の計算量は、ほぼO(n^3)と考えられる。
すると、2次元定常熱伝導の偏微分方程式を解く場合、格子点がn*n個の場合、係数行列のサイズがn^2となり、計算量はO(n^6)となって計算がすぐに事実上不可能になる。なお、メモリ量はO(n^4)となり、こちらも厳しい状態になる。

ところで、グラフを見て不審に思ったことはないだろうか。
あまりにも綺麗な曲線になっている。
それは、上で示したプログラムでは各サイズ1回だけ時間計測しているのだが、実際には20回計測して平均値を求めているので、滑らかになっている。1回だけだと、かなりギザギザになる。