Octaveで2次元定常熱伝導の偏微分方程式を解こう(4)

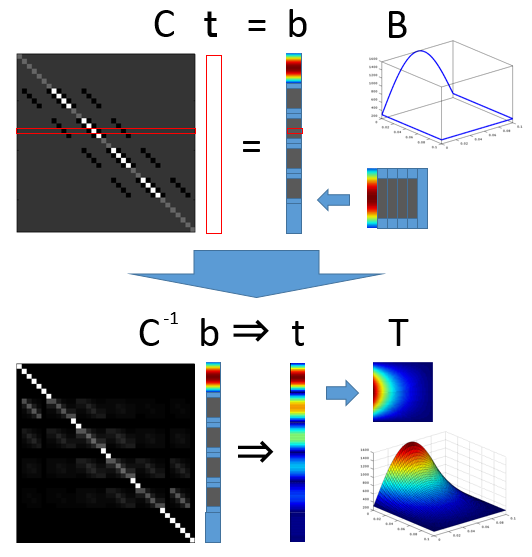
全体の流れを図にしてみた。
図中の赤枠は、格子点１つに対する偏微分方程式を示している。

1. まず、サイズNの正方行列Bの外周に対して温度を決める。
2. Bを列ベクトルｂに整形する。
3. サイズN*Nの正方行列（係数行列）を作る。
4. 係数行列の逆行列を両辺に左から掛けることで、温度列ベクトルtが求まる。
5. ｔをサイズNの正方行列Tに整形すると、全格子点の温度が求まる。

上図や今までに説明したことを元にプログラムを書くと、以下のようになる。
 

# ２元定常熱伝導の偏微分方程式を解こう

# 条件設定
TH = 1600;
T0 = 300;
N = 50; NN = N*N;
L = 0.1;
x = linspace(0,L,N);

# 境界条件の設定
B = zeros(N,N);
B(1,:)= B(N,:)= B(:,N) = T0;
B(1:N,1) = sin(pi*x/L)*(TH-T0) + T0;
b = reshape(B,NN,1);

# 係数行列の作成
C = full(gallery("poisson",N));
I = eye(NN);
C(1:N,:) = I(1:N,:);
C(1:N:NN,:) = I(1:N:NN,:);
C(N:N:NN,:) = I(N:N:NN,:);
C(NN-N+1:NN,:) = I(NN-N+1:NN,:);
C = sparse(C);

# 微分方程式を解く
t = C\b;
T = reshape(t,N,N);

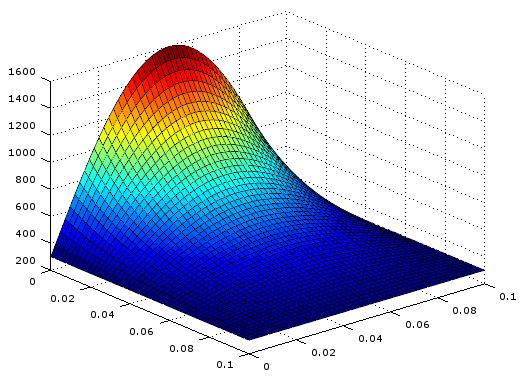
# 温度分布を図示
[X,Y] = meshgrid(x,x);
surf(X,Y,T);
view(50,30);

偏微分方程式の一番簡単な例を示してきたが、考え方が分かれば３次元化も可能であるが、格子点の数が劇的に多くなり、そのままでは殆んど計算できなくなってしまう。
対象領域が正方領域で、ｘ、ｙ両方をを同じ間隔で区切ったが、異なる間隔で区切ることも、対象領域が正方形ではなく長方形であっても、係数行列を工夫すれば計算可能になるのも分かるであろう。
さらに、対象領域が長方形でなく、任意な閉領域で、領域内の格子点に対して偏微分方程式が成り立つ場合も、面倒であるが同様にして計算できることが分かるであろう。
これらは、ここに書くのは面倒なので省略する。

次回は、別のことを書こうと思う。