簡単でない交叉処理
2013年 06月 03日
遺伝的アルゴリズムの説明で出てくる染色体は、int型の配列で表現されることが多い。
その代表例が、『ナップサック問題』である。
遺伝的アルゴリズムでは、2つの個体の染色体から、次の世代の個体の染色体を生成しなければいけない。
もとの2つの配列を、A、B、新しい配列をCとしたとき、C[i] = A[i] or B[i] とでもやっておけば済む。
実際の染色体のときのように、Aから適当な個数連続で取り、次にまたBから適当な個数連続で取るという風に工夫してもよい。
ナップサック問題は、ナップサックに詰め込む物をナップサックに入れるか入れないかなので、boolean配列で済ますことができる特別に簡単な場合である。通常は、各物について、重さと価値があり、ナップサックが耐えられる重さ以内で、最大価値の組み合わせを求めるものだ。
しかし、実際のナップサックに物を詰めるのは、そんなに簡単ではない。物には、サイズがあり、物をナップサックに詰めるというのは3次元空間に物を詰めるとても難しいパズルになってしまう。重いものは下に入れないと、物が潰れることもある。物によっては、配置方向が決まっていているものもあろう。現実は非常に複雑な制約があり、本物のナップサック問題を解くのは至難の技になる。
ということで、3次元パズルになってしまう現実的ナップサック問題を諦め、2次元パズルについて考えてみよう。
10×10のマス目を長方形に分割する問題を考えよう。分割するとき、各長方形には丸で示されている「核」が1つ入っていなければいけない。複数個入っていてはいけない。核の配置はあらかじめ決まっていて、勝手に動かしてはいけない。
次図の2つが、分割例である。


正しい分割が与えられると、環境順応性判定を行えるのだが、まだどちらも不十分と出た。
この2つの分割を両親とし、あたらしい分割を考えてみよう。
よく見ると、まったく同じ長方形がいくつか存在する。
どちらの親も同じになっている部分は、そのまま子にコピーすれば良いだろう。
ということで、次の図が得られる。
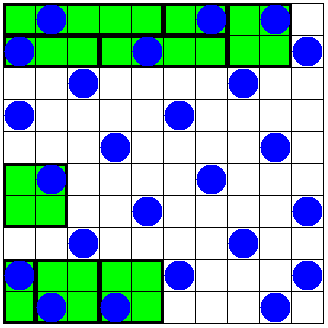
しかし、これでは未確定の部分がいっぱいで、子供ができない。
空白になっている部分をできるだけ両親の分割を反映させながら分割するにはどうすればよいだろうか?
その代表例が、『ナップサック問題』である。
遺伝的アルゴリズムでは、2つの個体の染色体から、次の世代の個体の染色体を生成しなければいけない。
もとの2つの配列を、A、B、新しい配列をCとしたとき、C[i] = A[i] or B[i] とでもやっておけば済む。
実際の染色体のときのように、Aから適当な個数連続で取り、次にまたBから適当な個数連続で取るという風に工夫してもよい。
ナップサック問題は、ナップサックに詰め込む物をナップサックに入れるか入れないかなので、boolean配列で済ますことができる特別に簡単な場合である。通常は、各物について、重さと価値があり、ナップサックが耐えられる重さ以内で、最大価値の組み合わせを求めるものだ。
しかし、実際のナップサックに物を詰めるのは、そんなに簡単ではない。物には、サイズがあり、物をナップサックに詰めるというのは3次元空間に物を詰めるとても難しいパズルになってしまう。重いものは下に入れないと、物が潰れることもある。物によっては、配置方向が決まっていているものもあろう。現実は非常に複雑な制約があり、本物のナップサック問題を解くのは至難の技になる。
ということで、3次元パズルになってしまう現実的ナップサック問題を諦め、2次元パズルについて考えてみよう。
10×10のマス目を長方形に分割する問題を考えよう。分割するとき、各長方形には丸で示されている「核」が1つ入っていなければいけない。複数個入っていてはいけない。核の配置はあらかじめ決まっていて、勝手に動かしてはいけない。
次図の2つが、分割例である。


正しい分割が与えられると、環境順応性判定を行えるのだが、まだどちらも不十分と出た。
この2つの分割を両親とし、あたらしい分割を考えてみよう。
よく見ると、まったく同じ長方形がいくつか存在する。
どちらの親も同じになっている部分は、そのまま子にコピーすれば良いだろう。
ということで、次の図が得られる。

しかし、これでは未確定の部分がいっぱいで、子供ができない。
空白になっている部分をできるだけ両親の分割を反映させながら分割するにはどうすればよいだろうか?



