プログラミングするのに数学の知識はあるに越したことはない。
でも、どのくらいあったら良いかの判断は難しい。
プログラミング言語の知識や、用意されているツール・ライブラリ等を使って、まあ少し勉強すれば出来ることをやるだけだったら、高等学校の数学すら不要と思う。
しかし、それでは、理屈は理解しないままプログラムをしているプログラマ程度で終ってしまう。
特に、AIに関するプログラムを書こうと思ってディープラーニングの本を開いたとたん、訳のわからないことだらけになる筈だ。
まず、理工系大学や高専で普通に教わる数学の共通部分程度の話にはついていけないと、非常に困る。
ということで、大学生向けに数学全般を扱ったシリーズ本を紹介しよう。
この分野、昔からピンからキリまで色々出ているのだが、あまりにも本格的になると大変だ。
数学専攻ならともかく、そうでない数学を道具として使いたい立場だと、やや軽めで、広く浅く、でもきちんとマスターすべきだ。
それで、今回は、このマセマシリーズを紹介しよう。


理工系大学の生協書籍部や大手書店の数学コーナーに行くと平積みされていることが多い本である。
帯には、東大・京大・東工大・早大・慶応大・・・ 大学生が一番読んでいる「キャンパスゼミ」シリーズです とある。
説明の仕方は、従来の大学の教科書とは大幅に違い、高校数学の受験参考書といった感じだ。
とにかく丁寧に書いていることは間違いない。
このシリーズで読むのが困難と言われたら困るのだが、文系の人でも大丈夫なように「大学基礎数学」があり、さらに高校数学レベルのシリーズもあるので、そのあたりからやれば誰でも大丈夫かな。
もちろん、いくつかの問題がある。
これは、あくまで入門参考書なので、レベルの高い部分はバサバサと切り捨てられている。
初めからもっと高度な本を読んでもよいし、これで基礎を固めてから、本来読むべき本格的な本に行っても良い。
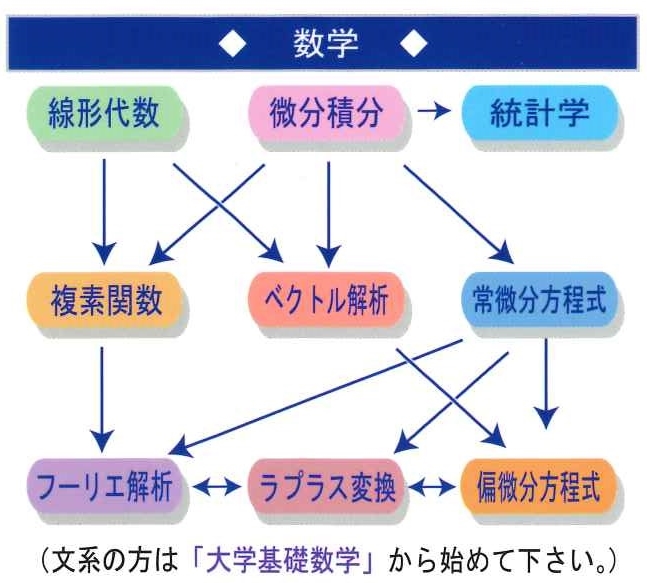
他のシリーズでもだいたい同様なのだが、マセマでは右図のような順番で勉強することを推奨しているようだ。
この「偏微分方程式」まで分かれば、ディープラーニングの原理もすっと分かるのではないかと思う。
AIをやるのだったら、確率・統計関係はもっとしっかり勉強しないとダメだろう。
もう1つ大きな問題は、本シリーズは大学理系共通で従来教えていた数学の範囲になっていて、情報系で必要とされている数学分野の多くが抜けていることだ。
思いついたままいい加減に並べてみると、整数論、離散数学、グラフ理論、代数学、数理論理学、、、、など色々あるし、さらに目指す分野によって違ってくる。
大学の情報系のシラバスを見ていると、これらはアルゴリズムの中に含まれていることが多いというか、アルゴリズムの中にあまりにも色々な分野が突っ込まれている感じがする。
この分野は、対象者が理工学全般に比べるとずっと少ないためか、シリーズというようなものはあまりないようだ。(あるのかな?)
ただの使い捨てプログラマなら数学は不要かも知れないが、エンジニアになるには数学は必須、知ってて当然だし、そうでないと深い理解が出来ず、効率的なプログラムなど書けない。
大学教養程度(1、2年)の数学は、参考書も多数あるし、ネットに転がっている無料コンテンツで勉強することも容易だ。
さらに、大学、先生によっては、講義ビデオが全部公開されていることも多いので、大いに利用しよう。
いや、それだけでなく、意欲ある高校生が高校の数学に嫌気がさして、大学の数学をかじってみるのもよい。
でも、どのくらいあったら良いかの判断は難しい。
プログラミング言語の知識や、用意されているツール・ライブラリ等を使って、まあ少し勉強すれば出来ることをやるだけだったら、高等学校の数学すら不要と思う。
しかし、それでは、理屈は理解しないままプログラムをしているプログラマ程度で終ってしまう。
特に、AIに関するプログラムを書こうと思ってディープラーニングの本を開いたとたん、訳のわからないことだらけになる筈だ。
まず、理工系大学や高専で普通に教わる数学の共通部分程度の話にはついていけないと、非常に困る。
ということで、大学生向けに数学全般を扱ったシリーズ本を紹介しよう。
この分野、昔からピンからキリまで色々出ているのだが、あまりにも本格的になると大変だ。
数学専攻ならともかく、そうでない数学を道具として使いたい立場だと、やや軽めで、広く浅く、でもきちんとマスターすべきだ。
それで、今回は、このマセマシリーズを紹介しよう。


理工系大学の生協書籍部や大手書店の数学コーナーに行くと平積みされていることが多い本である。
帯には、東大・京大・東工大・早大・慶応大・・・ 大学生が一番読んでいる「キャンパスゼミ」シリーズです とある。
説明の仕方は、従来の大学の教科書とは大幅に違い、高校数学の受験参考書といった感じだ。
とにかく丁寧に書いていることは間違いない。
このシリーズで読むのが困難と言われたら困るのだが、文系の人でも大丈夫なように「大学基礎数学」があり、さらに高校数学レベルのシリーズもあるので、そのあたりからやれば誰でも大丈夫かな。
もちろん、いくつかの問題がある。

これは、あくまで入門参考書なので、レベルの高い部分はバサバサと切り捨てられている。
初めからもっと高度な本を読んでもよいし、これで基礎を固めてから、本来読むべき本格的な本に行っても良い。
他のシリーズでもだいたい同様なのだが、マセマでは右図のような順番で勉強することを推奨しているようだ。
この「偏微分方程式」まで分かれば、ディープラーニングの原理もすっと分かるのではないかと思う。
AIをやるのだったら、確率・統計関係はもっとしっかり勉強しないとダメだろう。
もう1つ大きな問題は、本シリーズは大学理系共通で従来教えていた数学の範囲になっていて、情報系で必要とされている数学分野の多くが抜けていることだ。
思いついたままいい加減に並べてみると、整数論、離散数学、グラフ理論、代数学、数理論理学、、、、など色々あるし、さらに目指す分野によって違ってくる。
大学の情報系のシラバスを見ていると、これらはアルゴリズムの中に含まれていることが多いというか、アルゴリズムの中にあまりにも色々な分野が突っ込まれている感じがする。
この分野は、対象者が理工学全般に比べるとずっと少ないためか、シリーズというようなものはあまりないようだ。(あるのかな?)
ただの使い捨てプログラマなら数学は不要かも知れないが、エンジニアになるには数学は必須、知ってて当然だし、そうでないと深い理解が出来ず、効率的なプログラムなど書けない。
大学教養程度(1、2年)の数学は、参考書も多数あるし、ネットに転がっている無料コンテンツで勉強することも容易だ。
さらに、大学、先生によっては、講義ビデオが全部公開されていることも多いので、大いに利用しよう。
いや、それだけでなく、意欲ある高校生が高校の数学に嫌気がさして、大学の数学をかじってみるのもよい。



