標準的な巡回セールスマン問題は、経路長が最短のものを見つけるのであるが、これを変えてみた。
最適化の対象になる関数を適応度関数(fitness function)とか、コスト関数、評価関数とか呼ぶわけだが、このfitness関数を距離ではない次のようなものに変えてみた。
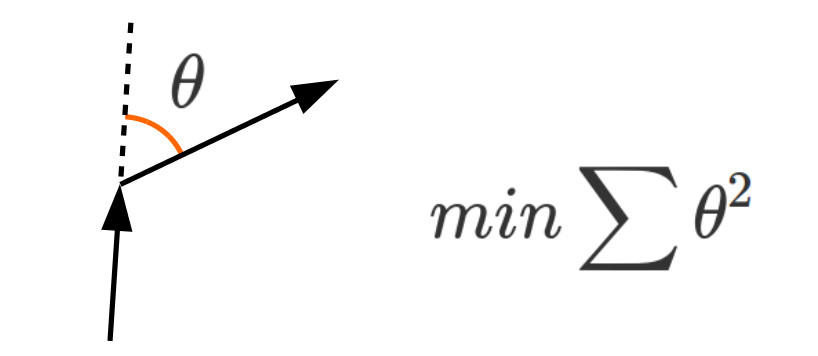
各頂点で曲がることになるのだが、そのときの回転角度の2乗和を最小にすることにした。
プログラムで変更したのはたったそれだけ。
すると、こんなことになった。 これは前のより点数が増えて500点であり、もっとぐるぐる回っているように見える。
これは前のより点数が増えて500点であり、もっとぐるぐる回っているように見える。
つまり、fitness関数は、なにか適当なのをでっちあげて、その関数の値を最適なもの(通常は最小か最大)を指定すると、後は延々と計算して、結果を表示してくれる。
ということで、巡回セールスマン問題だからといって、最短距離に凝り固まる必要はなく、ちょっと頭を柔軟にすると、色々なことを調べるのに使えるのだ。
巡回セールスマン問題は、実はもっともっと汎用性に富んでいるのだが、その話はまた次で。



