今回のあらすじ
SICPの3.3.3 Representing TablesのExercise 3.26とExercise 3.27を解きます。
Exercise 3.26
To search a table as implemented above, one needs to scan through the list of
records. This is basically the unordered list representation of section
2.3.3.
For large tables, it may be more efficient to structure the table in
a different manner. Describe a table implementation where the (key, value)
records are organized using a binary tree, assuming that keys can be ordered
in some way (e.g., numerically or alphabetically). (Compare exercise
2.66
of chapter 2.)
設計編
テーブルの内部表現を未ソートのリストから二分木に変えようという話です。
- 「a table as implemented above」はどこまで遡れば良いのか不明瞭なので、ここでは
前回解いた Exercise 3.25 で実装した可変次元テーブル
のことを指しているとしましょう
(問題文からすると1次元テーブルが相手でも構わないような気がしますが、
それだと簡単過ぎて詰まらないのですからね)。 - キーとしては数値を使うものだと仮定しましょう。
まずはテーブルの定義を整理しましょう。
前回実装した可変次元テーブルの場合、
- テーブル = 値 + レコードの集合
- レコード = キー + テーブル
でした。
レコードの作成は (cons key table) でできましたし、
レコードの集合への追加は (cons new-record record-set) でできましたから、
前回書いたコードはcons だの cdr だのがベタ書きされています。
これだと分かり辛くて仕方がないので、
- レコードの操作
- レコードの集合の操作
を明示的に手続き化して括り出しましょう。
そうすれば内部表現の変更はこれらの手続きを変更するだけで済みます。
リファクタリング編
まずはレコードを扱う手続きを定義しましょう:
(define (make-record key)
(cons key (make-table)))
(define record-key car)
(define record-table cdr)次にレコードの集合を扱う手続きを定義しましょう:
(define (make-record-set)
'())
(define empty-record-set? null?)
(define (lookup-record-set key record-set)
(assoc key record-set))
(define (adjoin-record-set! record record-set)
(cons record record-set))さらにテーブル関連の手続きもこの際なので整理しましょう:
(define (make-table)
(cons #f (make-record-set)))
(define table-value car)
(define set-table-value! set-car!)
(define table-record-set cdr)
(define set-table-record-set! set-cdr!)後は上記の手続きを使う形で前回書いた lookup や insert! を書き換えます:
(define (lookup keys table)
(define (go keys table)
(if (null? keys)
(table-value table)
(let ([record (lookup-record-set (car keys) (table-record-set table))])
(if record
(go (cdr keys) (record-table record))
#f))))
(go keys table))
(define (insert! keys value table)
(define (go keys table)
(if (null? keys)
(set-table-value! table value)
(let ([record (lookup-record-set (car keys) (table-record-set table))])
(cond
[record
(go (cdr keys) (record-table record))]
[else
(let ([new-record (make-record (car keys))])
(set-table-record-set! table (adjoin-record-set! new-record (table-record-set table)))
(go (cdr keys) (record-table new-record)))]))))
(go keys table)
'ok)実装編
さてここからが本題です。
整理に際して追加した手続き群が前提とする内部表現を未ソートのリストから二分木に変更するだけです。
まずはレコードの扱いから変えましょう:
(define (make-record key)
(list key (make-record-set) (make-record-set) (make-table)))
(define record-key car)
(define record-left cadr)
(define record-right caddr)
(define record-table cadddr)
(define (set-record-left! record record-set)
(set-car! (cdr record) record-set))
(define (set-record-right! record record-set)
(set-car! (cddr record) record-set))それとレコードの集合に関する手続きも少し追加しておきます:
(define (first-record record-set)
record-set)後は肝心の検索/追加の処理を二分木版にするだけです:
(define (lookup-record-set key record-set)
(if (empty-record-set? record-set)
#f
(let* ([record (first-record record-set)]
[rkey (record-key record)])
(cond [(< key rkey) (lookup-record-set key (record-left record))]
[(> key rkey) (lookup-record-set key (record-right record))]
[else record]))))
(define (adjoin-record-set! record record-set)
(if (empty-record-set? record-set)
record
(let* ([frecord (first-record record-set)]
[fkey (record-key frecord)]
[gkey (record-key record)])
(cond [(< gkey fkey)
(set-record-left! record-set (adjoin-record-set! record (record-left frecord)))]
[(> gkey fkey)
(set-record-right! record-set (adjoin-record-set! record (record-right frecord)))])
record-set)))Exercise 3.27
Memoization (also called tabulation) is a technique that enables
a procedure to record, in a local table, values that have previously been
computed. This technique can make a vast difference in the performance of
a program. A memoized procedure maintains a table in which values of
previous calls are stored using as keys the arguments that produced the
values. When the memoized procedure is asked to compute a value, it first
checks the table to see if the value is already there and, if so, just
returns that value. Otherwise, it computes the new value in the ordinary way
and stores this in the table. As an example of memoization, recall from
section
1.2.2
the exponential process for computing Fibonacci numbers:
(define (fib n)
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (fib (- n 1))
(fib (- n 2))))))The memoized version of the same procedure is
(define memo-fib
(memoize (lambda (n)
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (memo-fib (- n 1))
(memo-fib (- n 2))))))))where the memoizer is defined as
(define (memoize f)
(let ((table (make-table)))
(lambda (x)
(let ((previously-computed-result (lookup x table)))
(or previously-computed-result
(let ((result (f x)))
(insert! x result table)
result))))))Draw an environment diagram to analyze the computation of
(memo-fib 3).
Explain whymemo-fibcomputes the nth Fibonacci number in a number of
steps proportional to n. Would the scheme still work if we had simply
definedmemo-fibto be(memoize fib)?
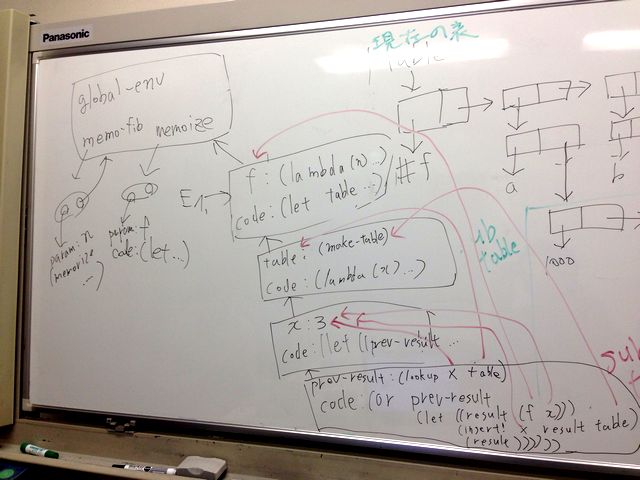
図
話を簡単にする為に引数の評価順序を左から右に行うものとすると、
大体以下のような感じになると思います:
-------------------------------------------------------------
| |
global-->| memoize: ... |
env | memo-fib:-. |
| / |
----------/--------------------------------------------------
^ | ^ ^ ^ ^ ^
| | | | | | |
,--+------+-------+---. -------- -------- -------- --------
| | | | | | n: 3 | | n: 2 | | n: 1 | | n: 0 |
v | | -----|-- -------- -------- -------- --------
@=@-' | E1-->|f:--' | ^ ^ ^ ^
| | -------- |E4 |E6 |E8 |E10
v | ^ (f 3) (f 2) (f 1) (f 0)
parameters: n | |
body: (cond ...) | ------------- -----------------
| | | | 0: 0 (via E9) |
,----------' E2-->|table: ------->| 1: 1 (via E7) |
| | | | 2: 1 (via E5) |
| | | | 3: 2 (via E3) |
| ------------- -----------------
| ^ ^ ^ ^ ^ ^
| | | | | | |
| | | | | | `----------------------------------------.
| | | | | `----------------------------. |
| ,--------------' | | `----------------. | |
| | ,------' `----. | | |
| | | | | | |
| | -------- -------- -------- -------- --------
| | | x: 3 | | x: 2 | | x: 1 | | x: 0 | | x: 1 |
| | -------- -------- -------- -------- --------
@=@-' ^ ^ ^ ^ ^ ^ ^ ^ ^ ^
| | |E3 | |E5 | |E7 | |E9 | |E11
| |(memo-fib 3) |(memo-fib 2) |(memo-fib 1) |(memo-fib 0) |(memo-fib 1)
| | | | | |
v ------------- ------------- ------------- ------------- -------------
parameters: x | result: 2 | | result: 1 | | result: 1 | | result: 0 | | result: 1 |
body: (let ...) ------------- ------------- ------------- ------------- -------------重要なのは (memo-fib 1) が2回評価されるところです。
1回目(E7)は (memo-fib 2) を評価する過程で行われ、
2回目(E11)は (memo-fib 3) を評価する過程で行われます。
2回目の評価では1回目の結果が再利用されます。
なので (memo-fib 0) の評価は全体で1回(E9)しか行われません。
何故nに比例するステップ数で計算できるか
例えば (fib 5) を評価する場合、以下のように再帰呼び出しが発生します:
(fib 5)
__________/ \__________
/ \
(fib 4) (fib 3)
___/ \___ / \
/ \ / \
(fib 3) (fib 2) (fib 2) (fib 1)
/ \ / \ / \
(fib 2) (fib 1) (fib 1) (fib 0) (fib 1) (fib 0)
/ \
(fib 1) (fib 0)これが memo-fib の場合、2回目以降は1回目の評価結果が再利用されます。
引数の評価順序が左から右だと仮定して、
上図のうち再利用される部分を [fib i] の形で明記すると以下のようになります:
(fib 5)
__________/ \__________
/ \
(fib 4) [fib 3]
___/ \___
/ \
(fib 3) [fib 2]
/ \
(fib 2) [fib 1]
/ \
(fib 1) (fib 0)つまり (memo-fib n) の評価で memo-fib が呼び出される回数は 2n – 1 回になります(n >= 2の場合)。
確かにnに比例するステップ数で計算できていますね
(実際の計算効率はテーブルの検索性能に左右されるのでO(n)とは言えない)。
memo-fib を (memoize fib) と定義した場合でも同じか
最初のバージョンの memo-fib だと i = 0…n に対して (fib i) の結果がメモされますが、(memoize fib) バージョンだと fib は内部的にメモ化されていない素の fib を呼ぶことになるので、(fib n) の最終結果だけがメモされることになります。
よってメモ化の恩恵を事実上受けられないことになります。
次回予告
3.3.4 A Simulator for Digital Circuits
をじっくり読んで時間内でできるだけ問題を解いて行きましょう。



