SICP読書会(Section 3.3.3 – Exercise 3.25)

今回のあらすじ

SICPの3.3.3 Representing Tablesを読んでExercise 3.25まで解きます。

3.3.3 Representing Tables

One-dimensional tables

要は連想配列です。
テキストに挙げられているのは素朴な実装なので簡単に理解できますね。

Two-dimensional tables

連想配列をネストさせて二次元にしたというだけです。
insert! は場合分けが増えて少々面倒臭いですが……

Creating local tables

Exercise 2.22とやってることは変わりませんね。
別の方法で実装し直したというだけです。

Exercise 3.24

In the table implementations above, the keys are tested for equality using
equal? (called by assoc). This is not always the appropriate test. For
instance, we might have a table with numeric keys in which we don’t need an
exact match to the number we’re looking up, but only a number within some
tolerance of it. Design a table constructor make-table that takes as an
argument a same-key? procedure that will be used to test “equality” of
keys. Make-table should return a dispatch procedure that can be used to
access appropriate lookup and insert! procedures for a local table.

要は

• キーの比較方法をカスタマイズできるようにする。
• 実装形態はテキスト中の “Creating local tables” のものと同じにする。

ということですね。
取り敢えずテキスト中の make-table をコピーして、
same-key? を取るようにしましょう:

(define (make-table same-key?)
  (let ((local-table (list '*table*)))
    (define (lookup key-1 key-2) ...)
    (define (insert! key-1 key-2 value) ...)
    (define (dispatch m) ...)
    dispatch))

テーブルの要素の検索は assoc で行われています。
assoc のキー比較は same-key? で行わせたいというのが今回の問題です。
assoc を使っている箇所はそのままで構わないのです。
ならここで作ったテーブルが使う assoc が equal? ではなく same-key? を使う特注版になっていれば十分ですね。
つまり、テキスト中の assoc の定義をこの make-table の中にコピーしてきて equal? を same-key? に置き換えればそれで完成です:

(define (make-table same-key?)
  (let ((local-table (list '*table*)))

    (define (assoc key records)
      (cond ((null? records) false)
            ((same-key? key (caar records)) (car records))
            (else (assoc key (cdr records)))))

    (define (lookup key-1 key-2) ...)
    (define (insert! key-1 key-2 value) ...)
    (define (dispatch m) ...)
    dispatch))

Exercise 3.25

設計編

Generalizing one- and two-dimensional tables, show how to implement a table
in which values are stored under an arbitrary number of keys and different
values may be stored under different numbers of keys. The lookup and
insert! procedures should take as input a list of keys used to access the
table.

「n次元テーブルを実装せよ」というだけなら話はまだ簡単なのですが、
問題は
“different values may be stored under different numbers of keys”
の一節です。nはテーブル毎に固定ではないのですね……
これにより割と面倒なケースが考えられます。
例えば以下のセッションについて考えてみましょう:

(define t (make-table))
(insert! '(a) 'x t)
(insert! '(a b c) 'z t)
(lookup '(a) t)      ;==> x
(lookup '(a b) t)    ;==> #f
(lookup '(a b c) t)  ;==> z

次元が固定ならn個のキー列に対してnレベル分テーブルを辿って値を探すだけなのですが、
このキー列の途中に値が挿入されている可能性もある訳です。
一体値をどう保持するのか熟慮する必要があります。

一次元テーブルの各要素はキーと値のペアでした。
二次元テーブルの場合は1レベル目のテーブルではキーとサブテーブルのペアで、
2レベル目のテーブルではキーと値のペアでした。
この問題で実装する可変次元テーブルの場合、
各要素は

• キー
• 値
• サブテーブル

で構成する必要があります。
この各要素は具体的にどういうデータ構造で保持しましょうか?
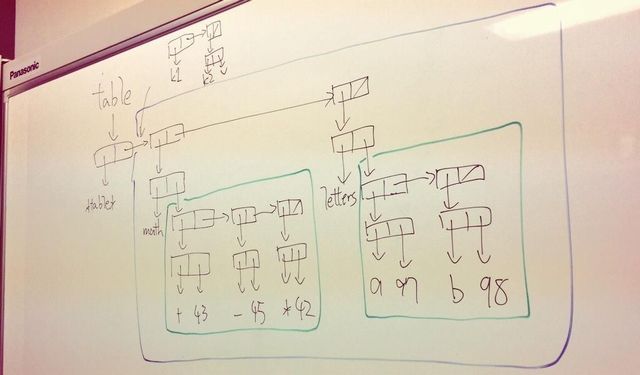
一先ずfigure 3.23の二次元テーブルの例をベースにして考えてみましょう:

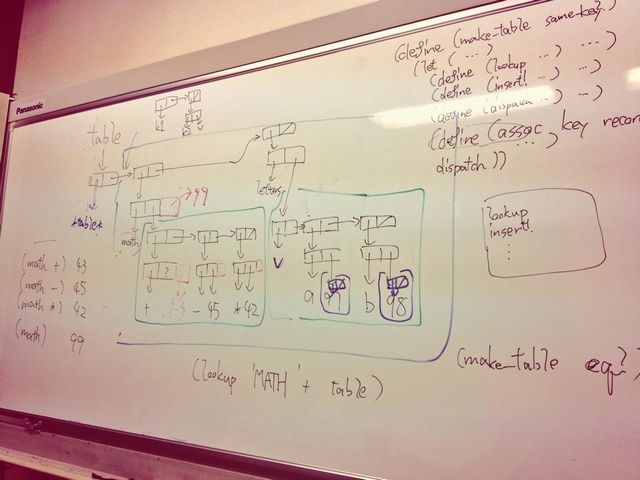
単純に各要素へ値を紐付けようとする(例えば上図の中央やや左 – math に対して 99 を紐付ける場合だ)と、
もはや cons では各要素を作れないのでconstructorを改めて定義する必要が出てきます。
必然的にselectorsやmutatorsについても考え直さなければなりません。
機能は実現できそうですが実装は面倒臭そうです。

という訳でもう一度テーブルについて考え直してみましょう。
最初にテキストで紹介された一次元テーブルは基本的に要素のリストで構成されていますが、
後からテーブルに値を追加できるようにする為、
要素リストの先頭にはさらなるconsセルが付いています。
そしてこの先頭のconsのcarは未使用でした。
なら各要素の値はこのcarに保持することにすれば良いのではないでしょうか?
(上図の中央やや右 – letters に対して v を紐付けている例)

こうすれば各要素はキーとテーブルのペアという形で統一されるので、
lookup や insert! も実装し易くなるはずです。

実装編

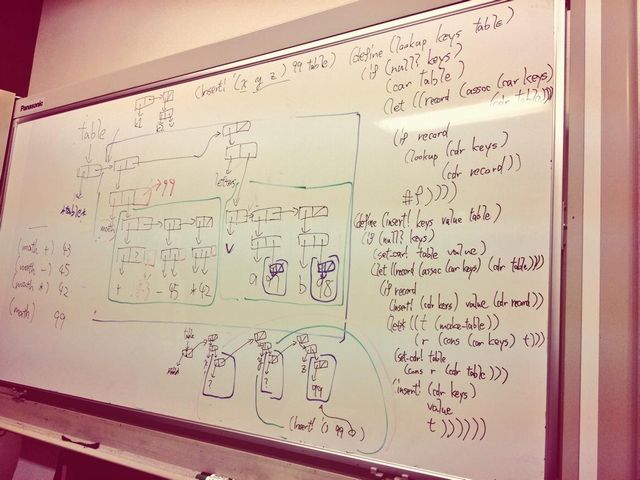
では最初に lookup を実装しましょう。
この可変次元テーブルだとテーブルが何段にも入れ子になっている形なので、
lookup を再帰的に呼べば良さそうです。つまり:

1. keys が空なら、適切なレベルのテーブルまで辿れたということなので、 table に格納された値を返す。
2. そうでないなら (car keys) で table の各要素を検索する。
   • 対応する要素が見つかったら、 (cdr keys) でその要素のテーブルを lookup する。
   • そうでなければ偽を返す。

という手順になります。後はこの lookup の手順をScheme語に翻訳すればOKです。

ただ、最初に例示したセッションについては要注意です:

(define t (make-table))
(insert! '(a) 'x t)
(insert! '(a b c) 'z t)
(lookup '(a) t)      ;==> x
(lookup '(a b) t)    ;==> #f
(lookup '(a b c) t)  ;==> z

この場合、 (a b) には何も値は登録されていないのですから lookup は偽を返すべきです。
ところが今回設計した可変次元テーブルだと (a b) は insert! されていないにも関わらず、
対応するテーブルと値が存在してしまうことになります。
今やテーブルのcarはダミーではなくなったのですから、
make-table では初期値として *table* の代わりに #f を使うとしましょう:

(define (make-table)
  (list #f))

これで上記のセッションのような使い方をされても大丈夫です。

次に insert! を実装しましょう。
これも lookup と同様に考えれば良さそうですが、
該当する要素が見つからなかった時は適宜コンテナーを作る必要があるところがややこしいですね。
手順としては以下の通りでしょう:

1. keys が空なら、適切なレベルのテーブルまで辿れたということなので、
   table に指定された value を登録する。
2. そうでなければ (car keys) で table の各要素を検索する。
   • 対応する要素が見つかったら、その要素のテーブルに対して (cdr keys) で value を insert! する。
   • そうでなければ新しい空のテーブルを作り、それと (car keys) で新しい要素を作り、その要素を table に追加する。その上で先程作った空テーブルに対して (cdr keys) で value を insert! する。

後はこの insert! の手順をScheme語に翻訳すればOKです。

うーん。 “Two-dimensional tables” で出てきたコードが面倒臭そうな感じだったので、
この可変次元テーブルも面倒臭そうなコードになるのかと思ってましたが、
データ構造をちゃんと考えておけば存外簡単なコードで実装できましたね。

次回予告

3.3.3 Representing TablesのExercise 3.26-3.27をじっくり解きます。
3.26は今回の内容を把握してないと解くのはかなり辛いのでしっかり復習しておきましょう。