SICP読書会(Exercise 3.34 – Exercise 3.37)

今回のあらすじ

SICPの3.3.5 Propagation of ConstraintsのExercise 3.34からExercise 3.37までサクサク解いていきます。

Exercise 3.34

Louis Reasoner wants to build a squarer, a constraint device with two
terminals such that the value of connector b on the second terminal will
always be the square of the value a on the first terminal. He proposes the
following simple device made from a multiplier:

(define (squarer a b)
  (multiplier a a b))

There is a serious flaw in this idea. Explain.

adder や multiplier と同様に、
squarer も一部のコネクター値が確定したら残りのコネクターの値を確定させることができます。
具体的には以下の2パターンがあります:

• a の値が確定したら、その二乗を b に設定する
• b の値が確定したら、その平方根を a に設定する

Louis の squarer は前者には対応しているものの後者には対応していません。

multiplier は p * q = r の制約でしかないので、
3つのコネクターのうち2つの値が確定しないと残り1つの値を確定させることが(基本的には)できません。
squarer が multiplier に同一のコネクター a を複数回使っていたとしても、
そのことを multiplier は知らない為、
Louis の squarer では平方根を求める事ができません。

Exercise 3.35

Ben Bitdiddle tells Louis that one way to avoid the trouble in exercise 3.34
is to define a squarer as a new primitive constraint. Fill in the missing
portions in Ben’s outline for a procedure to implement such a constraint:

(define (squarer a b)
  (define (process-new-value)
    (if (has-value? b)
        (if (< (get-value b) 0)
            (error "square less than 0 -- SQUARER" (get-value b))
            <alternative1>)
        <alternative2>))
  (define (process-forget-value) <body1>)
  (define (me request) <body2>)
  <rest of definition>
  me)

adder や multiplier と同じパターンで書けばいいので楽勝ですね:

(define (squarer a b)
  (define (process-new-value)
    (if (has-value? b)
        (if (< (get-value b) 0)
            (error "square less than 0 -- SQUARER" (get-value b))
            (set-value! a (sqrt (get-value b)) me))
        (if (has-value? a)
          (set-value! b (* (get-value a) (get-value a)) me))))
  (define (process-forget-value)
    (forget-value! a me)
    (forget-value! b me)
    (process-new-value))
  (define (me request)
    (cond ((eq? request 'I-have-a-value)
           (process-new-value))
          ((eq? request 'I-lost-my-value)
           (process-forget-value))
          (else
           (error "Unknown request -- SQUARER" request))))
  (connect a me)
  (connect b me)
  me)

Exercise 3.36

Suppose we evaluate the following sequence of expressions in the global
environment:

(define a (make-connector))
(define b (make-connector))
(set-value! a 10 'user)

At some time during evaluation of the set-value!, the following expression
from the connector’s local procedure is evaluated:

(for-each-except setter inform-about-value constraints)

Draw an environment diagram showing the environment in which the above
expression is evaluated.

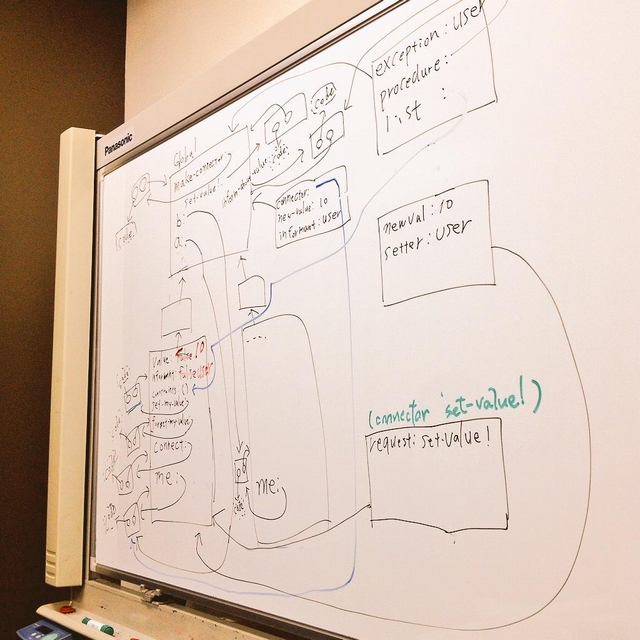
こんな感じですね:

右上隅が for-each-except を呼び出す時に作られたフレームです。

Exercise 3.37

The celsius-fahrenheit-converter procedure is cumbersome when compared with
a more expression-oriented style of definition, such as

(define (celsius-fahrenheit-converter x)
  (c+ (c* (c/ (cv 9) (cv 5))
          x)
      (cv 32)))
(define C (make-connector))
(define F (celsius-fahrenheit-converter C))

Here c+, c*, etc. are the “constraint” versions of the arithmetic
operations. For example, c+ takes two connectors as arguments and returns
a connector that is related to these by an adder constraint:

(define (c+ x y)
  (let ((z (make-connector)))
    (adder x y z)
    z))

Define analogous procedures c-, c*, c/, and cv (constant value) that
enable us to define compound constraints as in the converter example above.
[33]

c+ の実装と同様にすれば良いので楽勝ですね:

(define (c- x y)
  (let ((z (make-connector)))
    (adder z y x)
    z))

(define (c* x y)
  (let ((z (make-connector)))
    (multiplier x y z)
    z))

(define (c/ x y)
  (let ((z (make-connector)))
    (multiplier z y x)
    z))

(define (cv v)
  (let ((z (make-connector)))
    (constant v z)
    z))

しかし、制約システムの構築は面倒臭いものでしたが、このちょっとした変更だけで可読性が鰻登りです。
Schemeは凄いですね。

次回予告

3.4 Concurrency: Time Is of the Essenceをバリバリ読み進めます。
Exercise 3.38まで解けると良いかな……