最初に示したランダムに点を打つのを詳しく調べるために、丸を大きくし、順番に繋いでみた。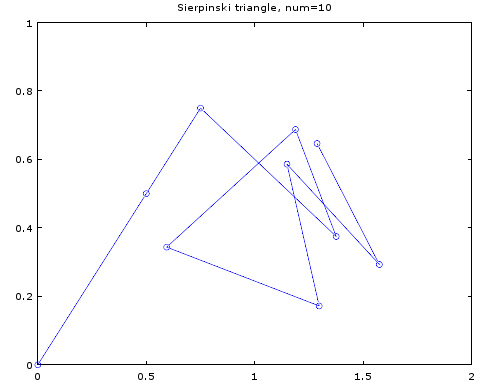
>> sierpinski2d_1
How many points: 10
(0.500000,0.500000)
(0.750000,0.750000)
(1.375000,0.375000)
(1.187500,0.687500)
(0.593750,0.343750)
(1.296875,0.171875)
(1.148438,0.585938)
(1.574219,0.292969)
(1.287109,0.646484)
これは、以下のプログラムを実行することで描かれる。
num = input("How many points: ");
x = 0;
y = 0;
X(1) = x;
Y(1) = y;
for i = 2:num
[x,y] = NextPoint(x,y);
X(i) = x;
Y(i) = y;
printf("(%f,%f)\n",x,y)
endfor
hold on
plot(X,Y,"ob") # 丸を描く
plot(X,Y) # 線で結ぶ
xlim([0,2])
ylim([0,1])
title( sprintf("Sierpinski triangle, num=%d",num) )
hold off描画点数Nを入力し、N個の点の座標を計算し、x座標、y座標をそれぞれ配列X,Yに溜め込んでから最後にプロットしているだけである。
プロットは、丸を描くのと、線で結ぶのを別々にしている。そのため、hold on/hold off により重ね描きを実現している。
次の点の座標を求める関数NextPointは以下のようになっている。
function [p,q] = NextPoint(x,y)
switch randi(3)
case 1
p = 0.5*x;
q = 0.5*y;
case 2
p = 0.5*x + 0.5;
q = 0.5*y + 0.5;
case 3
p = 0.5*x + 1;
q = 0.5*y;
endswitch
endfunction
この次の点の座標の計算の仕方(意図)の説明は今回は省略する。
その代わり、この乱数フラクタルと呼ばれる方法は、この本で見つけたのだが、もっと色々な切り口で説明を試みる。
つまり、この遣り方はエレガントでないし、汎用性にも乏しいことは次回に説明する。 Pythonからはじめる数学入門
Pythonからはじめる数学入門
Amit Saha 著
黒川 利明 訳
オライリー・ジャパン
2016/5/20 発行
A5, 304ページ
ISBN978-487311-768-3
第6章 幾何図形とフラクタルを描画する (p181-182)
問題6-2 シェルピンスキーの三角形
より計算方法を拝借した。



