Sierpinskiの三角形(6)

Sierpinskiの三角形を乱数フラクタルで描いた。でも、これは２次元である。今回は、３次元に拡張しよう。

前回のプログラムから３次元へは自然に拡張できる。

３次元に拡張したので、三角形が四角錐になる。ここでは、各辺の長さが同じの正四面体になるように、(0,0,0),(0,1,1),(1,0,1),(1,1,0)の４点を頂点として与えた。

まず、プログラムを示す。

num = input("How many points: ");
V = [ 0,0,0; 0,1,1; 1,0,1; 1,1,0 ];

P = [0,0,0];
X(1) = P(1);
Y(1) = P(2);
Z(1) = P(3);
for i = 2:num
    Q = V(randi(4),:);
    P = (P + Q)/2;
    X(i) = P(1);
    Y(i) = P(2);
    Z(i) = P(3);
endfor

plot3(X,Y,Z,".")

title( sprintf("Sierpinski pyramid, num=%d",num) )

1万点で描かせると、こういう風になる。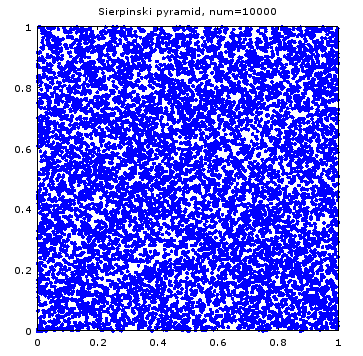



これだと、一辺１の正方形に点がランダムに散らばっているだけに見える。
でも、ちょっと視点を移動すると、点が立体的に散らばっていることが分かる。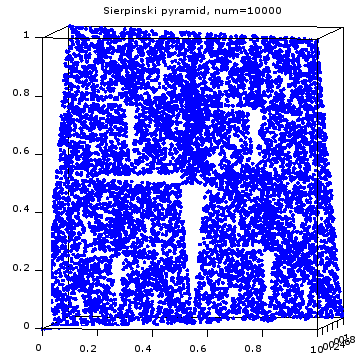


さらに視点を移動していくと、Sierpinskiの三角形が見えてくる。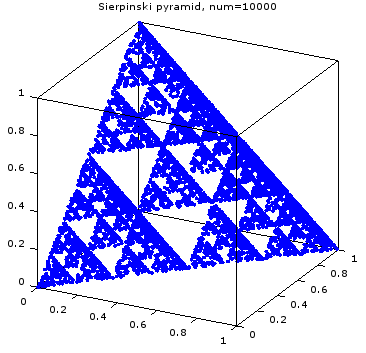



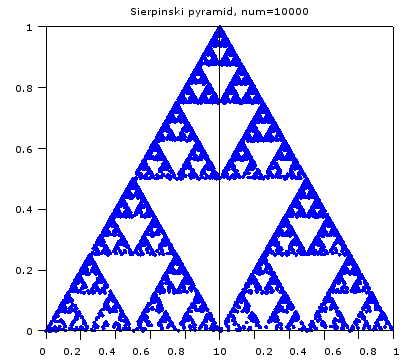
３次元図形は、結果を画像で見ても全然面白くない。マウスをグリグリすることで、見る方向がどんどん変わり、３次元を体感することがとても重要だ。ぜひ、Octave なり、MatLabを使ってみよう。

さて、何枚もの正四面体の図を示した。なので、もう一辺の長さが１の正四面体の面積の計算は簡単にできるようになったと思う。
個々で示した図には、横着（エレガント）な計算方法が示されている。この性質を利用した正四面体の体積計算は中学入試で出てくることもある。正四面体の底面積求めて高さを求めて体積を求めるとうい面倒なことは止めて、暗算可能な方法で教えよう。
詳しいことはネットにいっぱい説明があるので、自分で探そう。