SymPyで円周率をちゃんと計算してみよう

前回は、円周率を１００万桁、とても効率的というか、インチキというか、そういう方法で求めた。

今回は、真面目に円周率を計算する方法を考えてみよう。

円周率は、随分前から計算するための公式が分かっており、wikipediaにたくさん載っている。

昔から有名なのは、次のマチンの公式であろう。

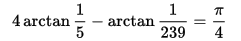これに基づいて計算すると、この程度の精度は出る。

In [397]: 4 * (4*atan(1/5) - atan(1/239))
Out[397]: 3.1415926535897936

しかし、これでは単に計算しただけに過ぎない。もっと精度を上げる工夫をしよう。

In [417]: expr = 4*(4 * atan(1/5) - atan(1/239))

In [418]: expr.evalf(50)
Out[418]: 3.1415926535897935600871733186068013310432434082031

これで５０桁表示できたようだ。前回のpiと比較してみよう。

In [419]: sympy.pi.evalf(50)
Out[419]: 3.1415926535897932384626433832795028841971693993751

ということで、全然一致していない。 どうやら、数式を計算してから、evalfで高精度にしても無駄のようだ。 なので、数式のままにしておいて、evalfの中で値を指定してみよう。

In [420]: expr = 4 * (4*atan(1/x) - atan(1/y))

In [421]: expr.evalf(50,subs={x:5,y:239})
Out[421]: 3.1415926535897932384626433832795028841971693993751

これで一応50桁は一致したようだ。 もうちょっと先の桁まで比較してみよう。 小数点以下１００万桁に挑戦。

In [430]: str(expr.evalf(1000001,subs={x:5,y:239}))[-50:]
Out[430]: '56787961303311646283996346460422090106105779458151'

In [431]: str(sympy.pi.evalf(1000001))[-50:]
Out[431]: '56787961303311646283996346460422090106105779458151'

これで１００万桁、ちゃんと計算できたようだ。めでたし、めでたし。
と思いたいところだが、単にatanを使って、桁数指定して計算しただけなので、やっぱりインチキ感は否めない。どうしよう。