SymPyで高性能な円周率の公式を使ったら計算が止まらない
2016年 11月 15日
円周率を延々と求めることが延々と行われてきた。そして、効率的に計算するための公式が次々と考案されてきた。桁数を上げようとすると、急激に計算量が増えてしまうのだった。
そのあたりを説明するときりがないので、詳しくは円周率(Wikipedia)を見よ。
しかし、どうやら最近は非常に効率のよい公式が見つかっているようだ。たとえば、これだ。
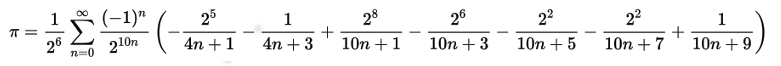 この収束は、2の10n乗分の1のペースのようだ。つまり、桁数nが増えても桁数に比例する程度の時間でしか計算量が増えないように思われる、なかなか画期的な公式だ。
この収束は、2の10n乗分の1のペースのようだ。つまり、桁数nが増えても桁数に比例する程度の時間でしか計算量が増えないように思われる、なかなか画期的な公式だ。
この公式の導き方を知りたい場合は、次を読もう。
A new formula to compute the n’th binary digit of pi, Fabrice Bellard, January 20, 1997
この公式を利用して、円周率を求めるPythonの関数を作ってみた。
桁数をパラメータlen で指定する。
項の加算を打ち切る限界は、桁数から決めた。
まず、とりあえず小数点以下50桁(全体で51桁)を求めてみた。
大丈夫なようだ。もっと桁数を増やしてみよう。
何が悪いんだろう。
そのあたりを説明するときりがないので、詳しくは円周率(Wikipedia)を見よ。
しかし、どうやら最近は非常に効率のよい公式が見つかっているようだ。たとえば、これだ。
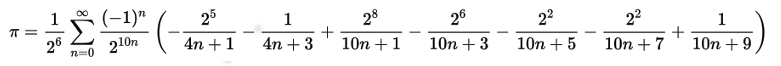 この収束は、2の10n乗分の1のペースのようだ。つまり、桁数nが増えても桁数に比例する程度の時間でしか計算量が増えないように思われる、なかなか画期的な公式だ。
この収束は、2の10n乗分の1のペースのようだ。つまり、桁数nが増えても桁数に比例する程度の時間でしか計算量が増えないように思われる、なかなか画期的な公式だ。この公式の導き方を知りたい場合は、次を読もう。
A new formula to compute the n’th binary digit of pi, Fabrice Bellard, January 20, 1997
この公式を利用して、円周率を求めるPythonの関数を作ってみた。
def FabriceBellard(len):
var('a:z')
term = (-1)**n/2**(10*n+6) * (-2**5/(4*n+1) - 1/(4*n+3) + 2**8/(10*n+1)
- 2**6/(10*n+3) - 2**2/(10*n+5) - 2**2/(10*n+7) + 1/(10*n+9))
sigma = 0
m = 0
while True:
t = term.evalf(len,subs={n:m})
if abs(t)<10**(-len):
break
sigma += t
m += 1
return sigma
桁数をパラメータlen で指定する。
項の加算を打ち切る限界は、桁数から決めた。
まず、とりあえず小数点以下50桁(全体で51桁)を求めてみた。
In [11]: FabriceBellard(51)
Out[11]: 3.14159265358979323846264338327950288419716939937511
In [12]: sympy.pi.evalf(51)
Out[12]: 3.14159265358979323846264338327950288419716939937511
大丈夫なようだ。もっと桁数を増やしてみよう。
In [19]: str(FabriceBellard(301))[-50:]
Out[19]: '45648566923460348610454326648213393607260249141274'
In [20]: str(sympy.pi.evalf(301))[-50:]
Out[20]: '45648566923460348610454326648213393607260249141274'
In [22]: str(FabriceBellard(401))[-50:]
^C---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
何が悪いんだろう。



