前回、SymPyでの連分数を作る関数
これを利用して計算してみよう。
連分数は、有理数だけではなく、無理数、超越数なども表せる。
まず練習として、2の平方根を求めてみよう。
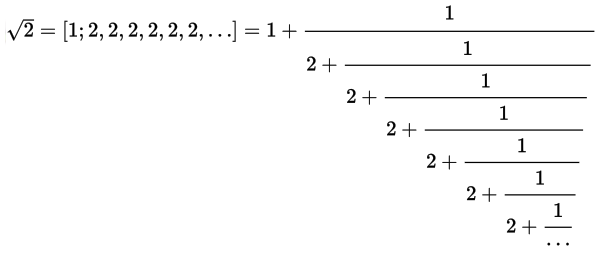 これから、2つのリストを[1,2,…]と[1,1,…]を作ることで2の平方根が求まる。
これから、2つのリストを[1,2,…]と[1,1,…]を作ることで2の平方根が求まる。
では、円周率を求めてみよう。Wikipediaに載っていた式をπについて整理すると次式を得る。
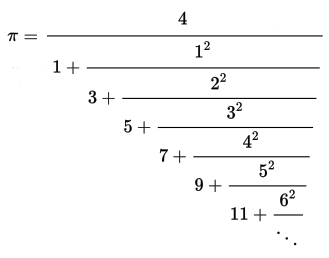 これを元に円周率は簡単に計算できる。
これを元に円周率は簡単に計算できる。
でも、それでは不満だろうから、ちょっと円周率を100万桁求められる方法を書いて終わりにする。
これを利用すると、1万桁でも、100万桁でも簡単に求まる。
以下では、最後の50桁だけ示した。
円周率100万桁までの本としては、以下の本が一部では非常に有名です。
円周 率1,000,000桁表
率1,000,000桁表
牧野貴樹 著
暗黒通信団 (2016/03) 発行
314円(本体)
ISBN-13: 978-4873100371
list_to_frac(A,B)を定義した。これを利用して計算してみよう。
連分数は、有理数だけではなく、無理数、超越数なども表せる。
まず練習として、2の平方根を求めてみよう。
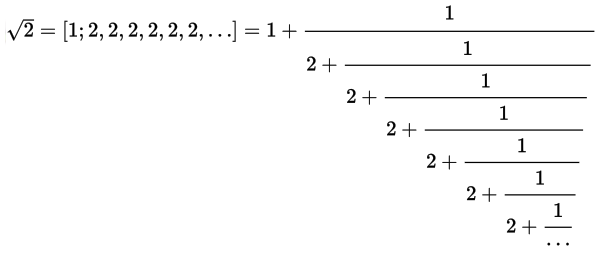 これから、2つのリストを[1,2,…]と[1,1,…]を作ることで2の平方根が求まる。
これから、2つのリストを[1,2,…]と[1,1,…]を作ることで2の平方根が求まる。In [91]: pa = [1]+[2]*20
In [92]: pa
Out[92]: [1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]
In [93]: pb = [1]*20
In [94]: pb
Out[94]: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
In [95]: list_to_frac(pa,pb)
Out[95]: 1.414213562373095
では、円周率を求めてみよう。Wikipediaに載っていた式をπについて整理すると次式を得る。
 これを元に円周率は簡単に計算できる。
これを元に円周率は簡単に計算できる。
n = 10
In [97]: pa = [0]+list(range(1,2*n,2))
In [98]: pa
Out[98]: [0, 1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
In [99]: pb = [4]+[x**2 for x in range(1,n+1)]
In [100]: pb
Out[100]: [4, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
In [101]: list_to_frac(pa,pb)
Out[101]: 3.14159254044654
In [103]: math.pi
Out[103]: 3.141592653589793
In [104]: n = 25
In [105]: pa = [0]+list(range(1,2*n,2))
In [106]: pb = [4]+[x**2 for x in range(1,n+1)]
In [107]: list_to_frac(pa,pb)
Out[107]: 3.141592653589793
でも、それでは不満だろうから、ちょっと円周率を100万桁求められる方法を書いて終わりにする。
In [108]: import sympy
In [109]: sympy.pi.evalf(20)
Out[109]: 3.1415926535897932385
これを利用すると、1万桁でも、100万桁でも簡単に求まる。
以下では、最後の50桁だけ示した。
In [115]: str(sympy.pi.evalf(10001))[-50:]
Out[115]: '46101264836999892256959688159205600101655256375678'
In [116]: str(sympy.pi.evalf(1000001))[-50:]
Out[116]: '56787961303311646283996346460422090106105779458151'
円周率100万桁までの本としては、以下の本が一部では非常に有名です。
円周
 率1,000,000桁表
率1,000,000桁表
牧野貴樹 著
暗黒通信団 (2016/03) 発行
314円(本体)
ISBN-13: 978-4873100371



