円周率の連分数展開
2012年 11月 30日
求めたい数といえば、やはり一番は円周率、πであろう。
円周率を正則連分数で示す方法もあるのだが、美しくない。
せっかく連分数を使っているし、円周率はもっと限りなく美しく表現できなければウソだ。
ということで、多くの数学者が研究しており、正則連分数ではないが、限りなく美しいものがある。
その1つがこれだ。
詳しくはWikipediaの連分数を見てほしい。
ここでは、この連分数をHaskellで計算することだけに集中する。
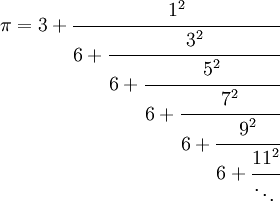
Haskellで実現するとき、延々と展開されていくところを、どう関数で表現するかだ。
最初を除けば、分数の頭にある6は固定値なので、そのまま書いてしまおう。
そして、今度は分数部分の分子が奇数で、どんどん増えていく。
この部分をどう実現しようか。
[1,3..] というリストを与えることで、実現できないだろうか。
√2を思い出そう。
let ratSqrt2 n = foldr (\x y -> x+1/y) (1%1) (1 : (take n [2,2..]))ここで、ラムダ関数を、
(\x y -> 6+x*x/y)
と書くだけで良いのではないだろうか。とりあえず、これで実験してみよう。
Prelude Data.List Data.Ratio> let pi' n = foldr (\x y -> 6+x*x/y) (1%1) (take n [1,3..])
Prelude Data.List Data.Ratio> pi' 10
16172869847 % 2633465835
Prelude Data.List Data.Ratio> fromRational (pi' 10)
6.141287132741557ちゃんと動いているようにも見えるが、整数部分が6になってしまっている。
ということで、リスト[1]が与えられた場合を考えてみよう。
すると、(\x y -> 6+x*x/y) に対して、 x=1, y=1 のときの値が結果として出てくる。
それは、 6+1*1/1 = 7 となる。
円周率の連分数展開では、最初だけなぜか3になっているので、3を引かないといけないので、全体から3を引くことにしよう。
Prelude Data.List Data.Ratio> let pi' n = (foldr (\x y -> 6+x*x/y) (1%1) (take n [1,3..]))-3
Prelude Data.List Data.Ratio> pi' 10
8272472342 % 2633465835
Prelude Data.List Data.Ratio> fromRational (pi' 10)
3.141287132741557
Prelude Data.List Data.Ratio> fromRational (pi' 20)
3.1415581036454996
Prelude Data.List Data.Ratio> fromRational (pi' 30)
3.1415827539476537
Prelude Data.List Data.Ratio> fromRational (pi' 50)
3.141590571791174
Prelude Data.List Data.Ratio> fromRational (pi' 100)
3.141592398533554
Prelude Data.List Data.Ratio> fromRational (pi' 500)
3.1415926515817754
Prelude Data.List Data.Ratio> fromRational (pi' 2000)
3.141592653558512
Prelude Data.List Data.Ratio> fromRational (pi' 10000)
3.1415926535895431万までやっても、どうも精度が怪しい。
Haskellでは、 pi とやるだけで実は円周率は使えるのだ。
Prelude Data.List Data.Ratio> pi
3.141592653589793この連分数展開は死ぬほど収束が遅いようだ。
はっきり言って、使い物にならない。
別の連分数展開に挑戦しよう。



